题目内容
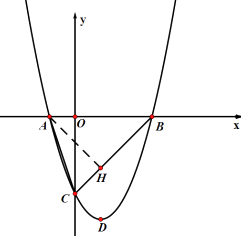
【题目】如图，在平面直角坐标系中，抛物线 
与 
轴交于A、B两点（点A在点B的左侧），点B的坐标为（3,0），与 
轴交于点C（0,-3），顶点为D。
（1）求抛物线的解析式及顶点D的坐标。
（2）联结AC，BC，求∠ACB的正切值。
（3）点P是x轴上一点，是否存在点P使得△PBD与△CAB相似，若存在，请求出点P的坐标；若不存在，请说明理由。
（4）M是抛物线上一点，点N在 轴，是否存在点N，使得以点A，C，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由。
【答案】
（1）
解：∵抛物线过点B（3，0）C（0，-3）
∴
解得：
∴抛物线解析式为：y=
-2x-3；
又∵ y=-2x-3=
-4；
∴顶点D的坐标为：D（1，-4）。
（2）
解：作AH⊥BC于点H
∵ -2x-3=0
解得：
=-1, 
=3
∴A(-1,0)
又∵OB=OC,∠B0C=90°
∴∠OBC=45°
∵AB=4
∴AH=BH=2
∵BC=3
∴CH=
∴tan∠ACB=
=2
（3）
解：作DG⊥OB于点G
∵BG=2,DG=4
∴tan∠DBG=2
∵tan∠ACB=2
∴∠DBG=∠ACB
当点P在点B的右侧时，∠PBD＞90°,
∴△PBD为钝角三角形与△CAB不相似
∴点P在点B的左侧
∴△PBD∽△CAB，且∠DBG=∠ACB
∴
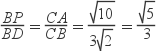
或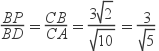
∵BD=2
∴BP=
或BP=6
∴P（-
，0）或P（-3，0）
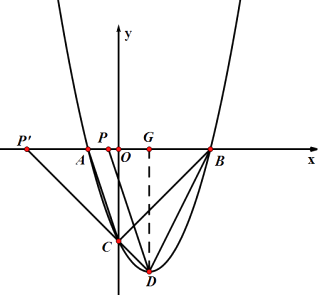
（4）
解：存在；N的坐标为：
(2+
,0); 
(2-,0) ; 
(-3,0)
【解析】（1）把点B与点C的坐标代入抛物线解析式，利用待定系数法求解，把解析式整理成顶点式即可写出顶点坐标；（2）首先得出A点坐标，进而得出∠OBC=45°，BC=3
， 再过点A做AH⊥BC,垂足为H，利用 tan∠ACB=
,求出即可；（3）根据平行四边形对边平行且相等的性质得出M及N点坐标；检验即可得出答案。
