题目内容
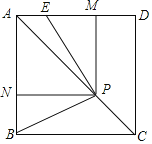
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
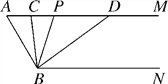
【答案】(1)60°;(2)不变,∠APB∶∠ADB=2∶1.,理由见解析;(3)∠ABC=30°
【解析】(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
解:(1)∵AM∥BN,∠A=60°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°.
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
(2)不变,∠APB∶∠ADB=2∶1.理由如下,
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB∶∠ADB=2∶1.
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN.
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°.

【题目】为充分利用雨水资源,幸福村的小明家和相邻的爷爷家采取了修建蓄水池、屋顶收集雨水的做法.已知小明和爷爷家的屋顶收集雨水的面积、蓄水池的容积和蓄水池已有水的量如下表:
小明家 | 爷爷家 | |
屋顶收集雨水的面积/m2 | 160 | 120 |
蓄水池的容积/ m3 | 50 | 13 |
蓄水池已有水的量/ m3 | 34 | 11.5 |
气象预报即将会下雨,为了收集尽可能多的雨水,下雨前需从爷爷家的蓄水池中抽取多少立方米的
水注入小明家的蓄水池?