Question

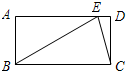
如图，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是（　　）

A． 1 2

B．1

C． 2

D． 3 2

Answer 1

在等腰RT△ACD和等腰RT△CBE中AD=CD，CE=BE，∠ACD=∠A=45°，∠ECB=∠B=45°
∴∠DCE=90°
∴AD²+CD²=AC²，CE²+BE²=CB²
∴CD²=

1

2

AC²，CE²=

1

2

CB2，
∵DE²=DC²+EC²，
∴DE=

1 2 AC2+ 1 2 CB2

=

2-AC×CB

=

(CB-1)2+1

∴当CB=1时，DE的值最小，即DE=1．
故选：B．