题目内容
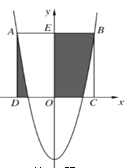
【题目】如图，二次函数y=2x2+m的图像经过点（0，-4），正方形ABCD的顶点C，D在x轴上，点A，B恰好在二次函数的图像上，则图中阴影部分的面积之和为_______.
【答案】8
【解析】
先把函数图象经过的点（0，-4）代入解析式求出m的值，再根据抛物线和正方形的对称性求出OD=OC，并判断出S阴影=S矩形BCOE，设点B的坐标为（n，2n）（n>0），把点B的坐标代入抛物线解析式求出n的值得到点B的坐标，然后求解即可．
∵二次函数y=2x2+m的图象经过点（0，-4），
∴m=-4，
∵四边形ABCD为正方形，
又∵抛物线和正方形都是轴对称图形，且y轴为它们的公共对称轴，
∴OD=OC，S阴影=S矩形BCOE，
设点B的坐标为（n，2n）（n>0），
∵点B在二次函数y=2x2-4的图象上，
∴2n=2n2-4，
解得，n1=2，n2=-1（舍负），
∴点B的坐标为（2，4），
∴S阴影=S矩形BCOE=2×4=8．
故答案为：8.
练习册系列答案
相关题目
