题目内容
【题目】如图(1)所示,在A,B两地间有一车站C,甲汽车从A地出发经C站匀速驶往B地,乙汽车从B地出发经C站匀速驶往A地,两车速度相同.如图(2)是两辆汽车行驶时离C站的路程y(千米)与行驶时间x(小时)之间的函数关系的图象.
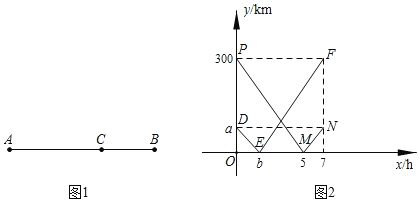
(1)填空:a= km,b= h,AB两地的距离为 km;
(2)求线段PM、MN所表示的y与x之间的函数表达式(自变量取值范围不用写);
(3)求行驶时间x满足什么条件时,甲、乙两车距离车站C的路程之和最小?
【答案】(1)120,2,420;(2)线段PM所表示的y与x之间的函数表达式是y=﹣60x+300,线段MN所表示的y与x之间的函数表达式是y=60x﹣300;(3)行驶时间x满足2≤x≤5时,甲、乙两车距离车站C的路程之和最小.
【解析】
(1)根据题意和图象中的数据,可以求得a、b的值以及AB两地之间的距离;
(2)根据(1)中的结果和函数图象中的数据,可以求得线段PM、MN所表示的y与x之间的函数表达式;
(3)根据题意,可以写出甲、乙两车距离车站C的路程之和和s之间的函数关系式,然后利用一次函数的性质即可解答本题.
(1)两车的速度为:300÷5=60km/h,
a=60×(7﹣5)=120,
b=7﹣5=2,
AB两地的距离是:300+120=420.
故答案为:120,2,420;
(2)设线段PM所表示的y与x之间的函数表达式是y=kx+b,
![]() ,得
,得![]() ,
,
即线段PM所表示的y与x之间的函数表达式是y=﹣60x+300;
设线段MN所表示的y与x之间的函数表达式是y=mx+n,
![]() ,得
,得![]() ,
,
即线段MN所表示的y与x之间的函数表达式是y=60x﹣300;
(3)设DE对应的函数解析式为y=cx+d,
![]() ,得
,得![]() ,
,
即DE对应的函数解析式为y=﹣60x+120,
设EF对应的函数解析式为y=ex+f,
![]() ,得
,得![]() ,
,
即EF对应的函数解析式为y=60x﹣120,
设甲、乙两车距离车站C的路程之和为skm,
当0≤x≤2时,
s=(﹣60x+300)+(﹣60x+120)=﹣120x+420,
则当x=2时,s取得最小值,此时s=180,
当2<x≤5时,
s=(﹣60x+300)+(60x﹣120)=180,
当5≤x≤7时,
s=(60x﹣300)+(60x﹣120)=120x﹣420,
则当x=5时,s取得最小值,此时s=180,
由上可得:
行驶时间x满足2≤x≤5时,甲、乙两车距离车站C的路程之和最小.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案