题目内容
【题目】如图1,四边形![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求四边形![]() 的面积;
的面积;
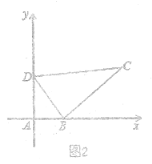
(2)如图2,以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 所在直线为
所在直线为![]() 轴、
轴、![]() 轴建立直角坐标系,点
轴建立直角坐标系,点![]() 在
在![]() 轴上,若
轴上,若![]() ,求
,求![]() 的坐标.
的坐标.
【答案】(1)36;(2)(0,0)或(0,8)
【解析】
(1)连接BD,根据勾股定理可以求得BD的长,然后根据勾股定理的逆定理可以判断△BDC的形状,从而可以解答本题;
(2)先根据![]() ,求出PD的长度,再根据D点的坐标即可求解.
,求出PD的长度,再根据D点的坐标即可求解.
解:(1)连接BD,
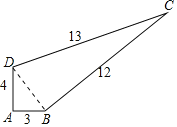
∵在△ABD中,∠DAB=90°,
∴BD2=AB2+AD2=32+42=25,
∴BD=5,
∵在△DBC中,DB2+BC2=52+122=25+144=169,CD2=132=169,
∴DB2+BC2=CD2,
∴△DBC是直角三角形,
∴∠DBC=90°,
∴S四边形ABCD=S△DAB+S△DBC=![]() ×3×4+
×3×4+![]() ×5×12=36.
×5×12=36.
(2)∵S△PBD=![]() S四边形ABCD,
S四边形ABCD,
∴![]() PDAB=
PDAB=![]() ×36=6,
×36=6,
∴![]() PD×3=6,
PD×3=6,
∴PD=4,
∵D(0,4),点P在y轴上,
∴P的坐标为(0,0)或(0,8).

练习册系列答案
 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目