题目内容
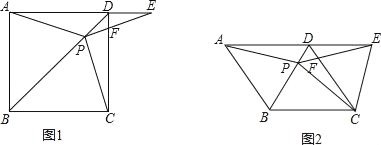
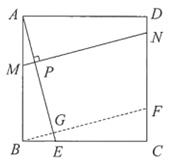
【题目】问题情境:如图1,在正方形ABCD中,E为边BC上一点(不与点B、C重合),垂直于AE的一条直线MN分别交AB、AE、CD于点M、P、N.判断线段DN、MB、EC之间的数量关系,并说明理由.
问题探究:在“问题情境”的基础上,
(1)如图2,若垂足P恰好为AE的中点,连接BD,交MN于点Q,连接EQ,并延长交边AD于点F.求∠AEF的度数;
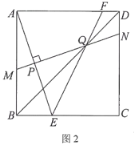
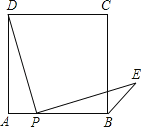
(2)如图3,当垂足P在正方形ABCD的对角线BD上时,连接AN,将△APN沿着AN翻折,点P落在点P'处.若正方形ABCD的边长为4 ,AD的中点为S,求P'S的最小值.
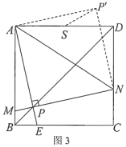
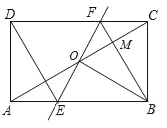
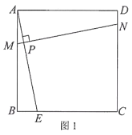
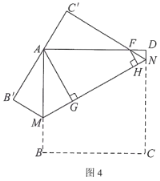
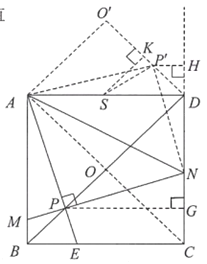
问题拓展:如图4,在边长为4的正方形ABCD中,点M、N分别为边AB、CD上的点,将正方形ABCD沿着MN翻折,使得BC的对应边B'C'恰好经过点A,C'N交AD于点F.分别过点A、F作AG⊥MN,FH⊥MN,垂足分别为G、H.若AG=![]() ,请直接写出FH的长.
,请直接写出FH的长.
【答案】问题情境:![]() .理由见解析;问题探究:(1)
.理由见解析;问题探究:(1)![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() ;问题拓展:
;问题拓展:![]() .
.
【解析】
问题情境:过点B作BF∥MN分别交AE、CD于点G、F,证出四边形MBFN为平行四边形,得出NF=MB,证明△ABE≌△BCF得出BE=CF,即可得出结论;
问题探究:(1)连接AQ,过点Q作HI∥AB,分别交AD、BC于点H、I,证出△DHQ是等腰直角三角形,HD=HQ,AH=QI,证明Rt△AHQ≌Rt△QIE得出∠AQH=∠QEI,得出△AQE是等腰直角三角形,得出∠EAQ=∠AEQ=45°,即可得出结论;
(2)连接AC交BD于点O,则△APN的直角顶点P在OB上运动,设点P与点B重合时,则点P′与点D重合;设点P与点O重合时,则点P′的落点为O′,由等腰直角三角形的性质得出∠ODA=∠ADO′=45°,当点P在线段BO上运动时,过点P作PG⊥CD于点G,过点P′作P′H⊥CD交CD延长线于点H,连接PC,证明△APB≌△CPB得出∠BAP=∠BCP,证明Rt△PGN≌Rt△NHP'得出PG=NH,GN=P'H,由正方形的性质得出∠PDG=45°,易得出PG=GD,得出GN=DH,DH=P'H,得出∠P'DH=45°,故∠P'DA=45°,点P'在线段DO'上运动;过点S作SK⊥DO',垂足为K,即可得出结果;
问题拓展:延长AG交BC于E,交DC的延长线于Q,延长FH交CD于P,则EG=AG=![]() ,PH=FH,得出AE=5,由勾股定理得出BE=
,PH=FH,得出AE=5,由勾股定理得出BE=![]() =3,得出CE=BC﹣BE=1,证明△ABE∽△QCE,得出QE=AE=
=3,得出CE=BC﹣BE=1,证明△ABE∽△QCE,得出QE=AE=![]() ,AQ=AE+QE=
,AQ=AE+QE=![]() ,证明△AGM∽△ABE,得出AM=
,证明△AGM∽△ABE,得出AM=![]() ,由折叠的性质得:AB'=EB=3,∠B'=∠B=90°,∠C'=∠BCD=90°,求出B'M=
,由折叠的性质得:AB'=EB=3,∠B'=∠B=90°,∠C'=∠BCD=90°,求出B'M=![]() ,AC'=1,证明△AFC'∽△MAB',得出AF=
,AC'=1,证明△AFC'∽△MAB',得出AF=![]() ,证明△DFP∽△DAQ,得出FP=
,证明△DFP∽△DAQ,得出FP=![]() ,得出FH=FP=
,得出FH=FP=![]() .
.
问题情境:因为四边形![]() 是正方形,
是正方形,
所以![]() .
.
过点![]() 作
作![]() 分别交
分别交![]() 于点
于点![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .所以
.所以![]() ,
,
所以![]() ,
,
又因为![]() ,
,
所以![]() .
.![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
问题探究:
(1)连接![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() 于点
于点![]() .易得四边形
.易得四边形![]() 矩形.
矩形.
所以![]() 且
且![]() .
.
因为![]() 是正方形
是正方形![]() 的对角线,所以
的对角线,所以![]() .
.
所以![]() 是等腰直角三角形,
是等腰直角三角形,![]() .所以
.所以![]() .
.
因为![]() 是
是![]() 的垂直平分线,所以
的垂直平分线,所以![]() .
.
所以![]() .所以
.所以![]() .
.
所以![]() .所以
.所以![]() .
.
所以![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,即
,即![]() .
.

(2)如图所示,连接![]() 交
交![]() 于点
于点![]() ,由题意易得
,由题意易得![]() 的直角顶点
的直角顶点![]() 在
在![]() 上运动.
上运动.
设点![]() 与点
与点![]() 重合,则点
重合,则点![]() 与点
与点![]() 重合;
重合;
设![]() 与点
与点![]() 重合,则点
重合,则点![]() 的落点为
的落点为![]() .易知
.易知![]() .
.
当点![]() 在线段
在线段![]() 上运动时,
上运动时,
过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
易证:![]() ,
,
所以![]() ,
,
因为![]() 是正方形
是正方形![]() 的对角线,
的对角线,
所以![]() ,易得
,易得![]() ,所以
,所以![]() .
.
所以![]() .
.
所以![]() ,故
,故![]() .
.
所以点![]() 在线段
在线段![]() 上运动.
上运动.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,因为点
,因为点![]() 为
为![]() 的中点,
的中点,
所以![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
问题拓展:
解:延长AG交BC于E,交DC的延长线于Q,延长FH交CD于P,如图4:

则EG=AG=![]() ,PH=FH,
,PH=FH,
∴AE=5,
在Rt△ABE中,BE=![]() =3,
=3,
∴CE=BC﹣BE=1,
∵∠B=∠ECQ=90°,∠AEB=∠QEC,
∴△ABE∽△QCE,
∴![]()
∵AG⊥MN,
∴∠AGM=90°=∠B,
∵∠MAG=∠EAB,
∴△AGM∽△ABE,
∴![]() ,即
,即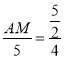 ,
,
解得:![]() ,
,
由折叠的性质得:AB'=EB=3,∠B'=∠B=90°,∠C'=∠BCD=90°,
∴B'M=![]() ,
,
∵∠BAD=90°,
∴∠B'AM=∠C'FA,
∴△AFC'∽△MAB',
∴ ,
,
解得:![]()
∵AG⊥MN,FH⊥MN,
∴AG∥FH,
∴AQ∥FP,
∴△DFP∽△DAQ,
∴![]() ,即
,即 ,
,
解得:FP=![]() ,
,
∴FH=![]() .
.