题目内容
以锐角△ABC的边AC、AB为边向外作正方形ACDE和正方形ABGF,连结BE、CF,
(1)试探索BE和CF长度的关系?并证明;
(2)你能找到哪两个图形可以通过旋转而互相得到,并指出旋转中心和旋转角。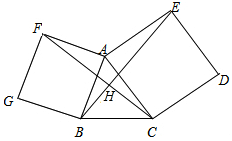
(1)试探索BE和CF长度的关系?并证明;
(2)你能找到哪两个图形可以通过旋转而互相得到,并指出旋转中心和旋转角。

(1)BE=CF;(2)△FAC与△BAE,旋转中心为点A、旋转角为90°
试题分析:(1)由正方形ACDE和正方形ABGF可得AF=AB, AE=AC,∠FAB=∠EAC=90°,即可得到∠FAC=∠BAE,从而证得△FAC≌△BAE,结论得证;
(2)由(1)可得△FAC≌△BAE,再结合旋转的定义即可得到结果.
(1)∵正方形ABGF,正方形ACDE,
∴AF=AB, AE=AC,∠FAB=∠EAC=90°,
∵∠FAC=∠FAB+∠BAC,
∠BAE=∠EAC+∠BAC,
∴∠FAC=∠BAE,
∴△FAC≌△BAE,
∴BE=CF;
(2)由(1)知,△FAC≌△BAE,
故△FAC和△BAE可以通过旋转而得到彼此,
其旋转中心为点A,旋转角为90°.
点评:解答本题的关键是熟练掌握正方形的四条边相等,四个角均是直角;同时熟记旋转的定义:在平面内,把一个图形绕点O旋转一个角度的图形变换叫做旋转,点O叫做旋转中心,旋转的角叫做旋转角.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
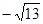 用字母
用字母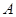 表示出来。
表示出来。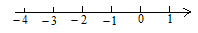
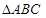 ,使得顶点
,使得顶点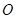 处,再把所得到的三角形以点
处,再把所得到的三角形以点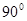 ,画出平移和旋转后得到的两个图形。
,画出平移和旋转后得到的两个图形。


 中,
中,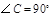 ,
,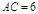 ,
, ,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于E,交斜边于F,则
,将它的一个锐角翻折,使该锐角顶点落在其对边的中点D处,折痕交另一直角边于E,交斜边于F,则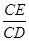 的值为 .
的值为 . 绕点
绕点 逆时针旋转
逆时针旋转 到
到 的位置,已知
的位置,已知 ,则
,则 等于( )
等于( )




 中,
中, ,点
,点 在边
在边 上,且
上,且 将
将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 连结
连结 下列结论:①
下列结论:① ②
②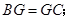 ③
③ ④
④

 ,点
,点 都在格点上.
都在格点上. 的长;
的长; ,求
,求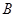 点的对应点
点的对应点 的坐标;
的坐标; 关于坐标原点对称的点
关于坐标原点对称的点 ,并写出点
,并写出点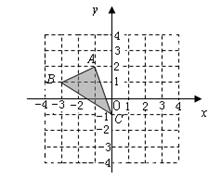
 是正方形,
是正方形, 旋转后与
旋转后与 重合。
重合。
 的形状。(不要求证明)
的形状。(不要求证明)