题目内容
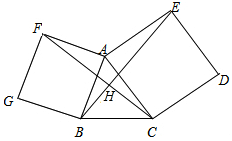
如图,正方形 中,
中, ,点
,点 在边
在边 上,且
上,且 将
将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 连结
连结 下列结论:①
下列结论:① ②
②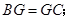 ③
③ ④
④
其中正确结论的个数是 ( )

 中,
中, ,点
,点 在边
在边 上,且
上,且 将
将 沿
沿 对折至
对折至 ,延长
,延长 交边
交边 于点
于点 连结
连结 下列结论:①
下列结论:① ②
②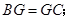 ③
③ ④
④
其中正确结论的个数是 ( )

| A.1 | B.2 | C.3 | D.4 |
C
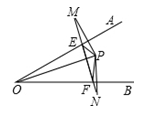
试题分析:根据折叠的性质和正方形的性质可证Rt△ABG≌Rt△AFG;在直角△ECG中,根据勾股定理可证BG=GC;先证得∠AGB=∠AGF=∠GFC=∠GCF,由平行线的判定可得AG∥CF;由于

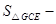
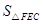 ,求得面积比较即可.
,求得面积比较即可.∵AB=AD=AF,AG=AG,∠B=∠AFG=90°,
∴Rt△ABG≌Rt△AFG(HL),故①正确;∵EF=DE=
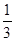 CD=2,设BG=FG=x,则CG=6-x.
CD=2,设BG=FG=x,则CG=6-x.在直角△ECG中,根据勾股定理,得
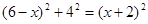 ,解得x=3
,解得x=3所以BG=3=6-3=GC,故②正确;
∵CG=BG,BG=GF,
∴CG=GF,
∴△FGC是等腰三角形,∠GFC=∠GCF.
又∵Rt△ABG≌Rt△AFG;
∴∠AGB=∠AGF,∠AGB+∠AGF=180°-∠FGC=∠GFC+∠GCF,
∴∠AGB=∠AGF=∠GFC=∠GCF,
∴AG∥CF,故③正确;
 ,GF=3,EF=2,△GFC和△FCE等高,
,GF=3,EF=2,△GFC和△FCE等高,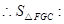
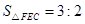 ,
,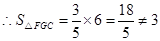 ,故④错误;
,故④错误;故选C.
点评:解答此题的关键是熟练掌握折叠的性质:折叠前后图形的形状和大小不变,对应边和对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,连接
,连接 ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
 ,PB=1,PD=
,PB=1,PD= ,则∠APB的度数等于 ,正方形的边长为 ;
,则∠APB的度数等于 ,正方形的边长为 ; ,PB=1,PF=
,PB=1,PF=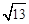 ,则∠APB的度数等于 ,正六边形的边长为 .
,则∠APB的度数等于 ,正六边形的边长为 .