题目内容
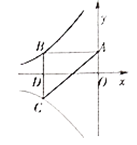
【题目】如图,直线ykx3经过点B(-![]() ,2),且与 x 轴交于点A.将抛物线
,2),且与 x 轴交于点A.将抛物线 ![]() 沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿 x 轴作左右平移,记平移后的抛物线为C,其顶点为P.
(1)求∠OAB 的度数;
(2)抛物线![]() 与直线 ykx3相交于 M,N两点,求△MON的面积.
与直线 ykx3相交于 M,N两点,求△MON的面积.
(3)在抛物线![]() 平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
平移过程中,将△PAB 沿直线 AB 翻折得到△DAB,点D 能否落在抛物线C 上?如能,求出此时抛物线C 顶点P 的坐标;如不能,说明理由.
【答案】(1)30°(2)![]() (3)(3
(3)(3![]() ,0)
,0)
【解析】分析:(1)点B在直线AB上,所以把B点坐标代入解析式即可求出未知数的值,进而求出其解析式.根据直线解析式可求出A点的坐标及直线与y轴交点的坐标,根据锐角三角函数的定义即可求出∠BAO的度数.
(2)设![]() 联立
联立 消去y,得到
消去y,得到![]() ,则
,则![]() ,
,![]() ,
,![]() ,即可求得
,即可求得![]() .
.
(3)根据特殊角求出D点的坐标表达式,将表达式代入解析式,看能否计算出P点坐标,若能,则D点在抛物线C上.反之,不在抛物线上.
详解:(1)∵点B在直线AB上,求得b=3,
∴直线AB:![]() ,
,
∴A(![]() ,0),即OA=
,0),即OA=![]() .
.
当![]() 时,直线AB:
时,直线AB:![]() 与
与![]() 轴交于点
轴交于点![]()
∴![]() .
.
(2) 设![]()
联立 消去y,得到
消去y,得到![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 于y轴相交于(0,3)
于y轴相交于(0,3)
∴![]()
(3)假设点D落在抛物线C上,
不妨设此时抛物线顶点P(t,0),则抛物线C:![]() ,AP=
,AP=![]() + t,
+ t,
连接DP,作DM⊥x轴,垂足为M.由已知,得△PAB≌△DAB,
又∠BAO=30°,∴△PAD为等边三角形.PM=AM=![]() ,
,
∴![]()
![]() ,
,
![]() .
.
∵点D落在抛物线C上,
∴![]()
当![]() 时,此时点P
时,此时点P![]() ,点P与点A重合,不能构成三角形,不符合题意,舍去.所以点P为(
,点P与点A重合,不能构成三角形,不符合题意,舍去.所以点P为(![]() ,0)
,0)
∴当点D落在抛物线C上顶点P为(![]() ,0).
,0).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目