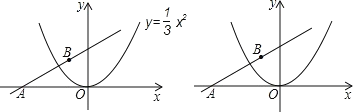Question

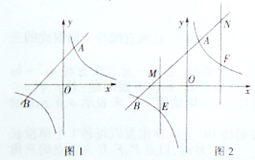
【题目】如图1所示,一次函数y=kx+b的图象与反比例函数y= 的图象交A(1,4)，B(-4,c)两点,

(1)求反比例函数及一次函数的解析式;

(2)点P是x轴上一动点,使|PA-PB|的值最大,求点P的坐标及△PAB的面积;

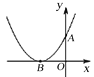
(3)如图2所示,点M、N都在直线AB上,过M、N分别作y轴的平行线交双曲线于E、F,设M、N的横坐标分别为m、n,且, ,请探究,当m、n满足什么关系时，ME=NE.

Answer 1

【答案】（1）反比例函数的解析式为y=，一次函数的解析式为y=x+3；（2）P点坐标为(-,0)，S△PAB=；（3）当mn=-4时,ME=NE.

【解析】试题分析：

（1）把点A（1，4）、B(-4，c)的坐标分别代入反比例函数的解析式，即可求得反比例函数的解析式和c的值，从而可得点B的坐标，再把A、B的坐标代入一次函数的解析式求得k、b的值即可得到一次函数的解析式；

（2）作点B关于x轴的对称点B′，连接AB′交x轴于点P，此时所得点P为所求点，先由A和B′的坐标求出直线AB′的解析式，再求点P的坐标，再求出直线AB与x轴的交点坐标即可求得△PAB的面积了；

（3）由题意可得用“m”和“n”的式子分别表达出点M和点N的坐标，进而可表达出ME和NF的长度，结合ME=NF可得关于“m、n”的等式，把等式变形即可得到所求结论.

试题解析：

(1)把A(1,4)代入y= ,得4= , ∴a=4.

∴反比例函数的解析式为y=

把B(-4,c)代入,得c= =-1.∴B(-4,-1).

把A(1,4)、B(-4,-1)代入y=kx+b得

∴

∴一次函数的解析式为y=x+3.

(2)如图所示,作B关于x轴的对称点B,则B'(-4,1),连接AB并延长交x轴于P,则此时|PA-PB|的值最大.设直线AB'的解析式为y=k1x+b1,则有

∴

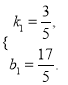
∴直线AB′的解析式为y=x+ ,当y=0

时,x=-

∴P点坐标为(-,0)

∵直线AB与x轴的交点为(-3,0),

S△PAB=；

(3)由题可知，M(m,m+3)，N(n,n+3)，E ，

∵.-4<m<0，n>1，

∴ME=m+3 ，NF=n+3，

当ME=NF时，m+3- =n+3- ，即

∴,m≠n，

∴mn=-4.

∴当mn=-4时，ME=NE.