题目内容
将图①中的正方形剪开得到图②，图②中共有4个正方形；将图②中一个正方形剪开得到图③，图③中共有7个正方形；将图③中一个正方形剪开得到图④，图④中共有10个正方形；…；如此下去，则第2014个图中共有正方形的个数为（ ）
| A、2014 | B、2017 | C、6040 | D、6044 |
考点：规律型：图形的变化类
专题：
分析：观察图形可知，每剪开一次多出3个正方形，然后写出前4个图形中正方形的个数，再根据此规律写出第n个图形中的正方形的个数的表达式，再代入2014求得问题即可．
解答：解：第1个图形有正方形1个，
第2个图形有正方形4个，
第3个图形有正方形7个，
第4个图形有正方形10个，
…，
第n个图形有正方形（3n-2）个．
则第2014个图中共有正方形的个数为3×2014-2=6040．
故选：C．
第2个图形有正方形4个，
第3个图形有正方形7个，
第4个图形有正方形10个，
…，
第n个图形有正方形（3n-2）个．
则第2014个图中共有正方形的个数为3×2014-2=6040．
故选：C．
点评：此题考查图形的变化规律，通过观察图形，分析、归纳发现其中的规律，并应用规律解决问题．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
设n是任意一个整数，下列说法错误的是（ ）
| A、任意一个偶数都可用4n表示 | B、有的偶数不能用4n表示 | C、2n可以表示任一个偶数 | D、n的奇数倍不一定是奇数 |
a+b=-3，c+d=2，则（c-b）-（a-d）的值为（ ）
| A、5 | B、-5 | C、1 | D、-1 |
一列数a1，a2，a3，…，其中a1=1．an=
（n为大于1的整数），则a4等于（ ）
| 1 |
| 1+an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，M、N是正五边形ABCDE各边上的两个动点，若它们分别从顶点A、D出发，同时沿正六方形的边移动，M点以顺时针方向移动，N点以逆时针方向移动，假设点M的速度是点N的速度的5倍，则它们2012次相遇在（ ）边上．| A、AE | B、ED | C、CD | D、BC |
把边长为1的正方形按如图所示的方式排列，则第n个图形的周长用含n（n为正整数）的式子表示为（ ）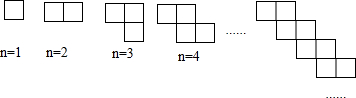
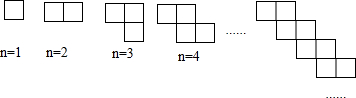
| A、4n | B、2n-2 | C、2n+2 | D、4n-4 |
已知关于x的方程2x-m+5=0的解是x=-2，则m的值为（ ）
| A、1 | B、-1 | C、9 | D、-9 |
骰子可以看做是一个小立方体（如图），它相对两面之和的点数之和是7，下面展开图中符合规则的是（ ）
