题目内容
如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C′处;作∠BPC′的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )
A. | B. | C. | D. |
C.
解析试题分析:∵将△PCD沿直线PD折叠,使点C落下点C′处;
∴∠CPD=∠C′PD= ∠CPC′,
∠CPC′,
∵PE平分∠BPC′,
∴∠BPE=∠C′PE= ∠BPC′,
∠BPC′,
又∵∠BPC′+∠CPC′=180°,,
∴∠BPE+∠CPD=90°,
在△PCD中,
∵∠C=90°,
∴∠CPD+∠PDC=90°,
∴∠BPE=∠PDC,
又∵∠B=∠C=90°,
∴△PCD∽△EBP,
∴ ,
,
即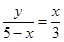 ,
,
∴y= x(5﹣x)=﹣
x(5﹣x)=﹣ (x﹣
(x﹣ )2+
)2+ ,
,
只有C选项图象符合.
故选C.
考点:动点问题的函数图象.

练习册系列答案
相关题目
如图是二次函数y=ax2+bx+c图象的一部分,且过点A(3,0),二次函数图象的对称轴是x=1,下列结论正确的是( )
| A.b2>4ac | B.ac>0 | C.a﹣b+c>0 | D.4a+2b+c<0 |
已知0≤x≤ ,那么函数y=﹣2x2+8x﹣6的最大值是( )
,那么函数y=﹣2x2+8x﹣6的最大值是( )
| A.﹣10.5 | B.2 | C.﹣2.5 | D.﹣6 |
二次函数y=ax2+bx-1(a≠0)的图象经过点(1,1).则代数式1-a-b的值为( )
| A.-3 | B.-1 | C.2 | D.5 |
如图,已知抛物线与x轴的一个交点为A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
| A.(-3,0) | B.(-2,0) |
| C.x=-3 | D.x=-2 |
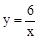 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
 CPD 的面积为y. 则下列图象中,能表示y与x的函数关系的图象大致是( )
CPD 的面积为y. 则下列图象中,能表示y与x的函数关系的图象大致是( )
 B.
B.  C.
C.  D.
D.
