题目内容
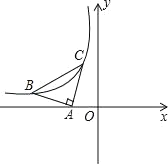
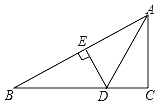
【题目】如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于点D,DE恰好是AB的垂直平分线,垂足为E.若BC=6,则AB的长为( )
A.3![]() B.4
B.4![]() C.8D.10
C.8D.10
【答案】B
【解析】
根据角平分线的性质得到∠BAD=∠CAD,根据线段垂直平分线的性质、三角形内角和定理得到∠DBA=30°,根据含30度角的直角三角形的性质、勾股定理计算即可.
解:∵AD是∠CAB的平分线,
∴∠BAD=∠CAD,
∵DE是AB的垂直平分线,
∴DB=DA,
∴∠BAD=∠DBA,
∴∠BAD=∠DBA=∠CAD,
∵∠C=90°,
∴∠BAD=∠DBA=∠CAD=30°,
∴AB=2AC,
由勾股定理得,AB2﹣AC2=BC2,
即![]()
解得,AB=4![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?