题目内容
【题目】如图,已知抛物线y=﹣![]() x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.
x2+bx+c与x轴交于原点O和点A(6,0),抛物线的顶点为B.
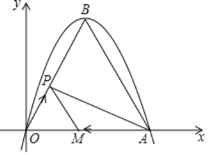
(1)求该抛物线的解析式和顶点B的坐标;
(2)若动点P从原点O出发,以每秒1个长度单位的速度沿线段OB运动,设点P运动的时间为t(s).问当t为何值时,△OPA是直角三角形?
(3)若同时有一动点M从点A出发,以2个长度单位的速度沿线段AO运动,当P、M其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t(s),连接MP,当t为何值时,四边形ABPM的面积最小?并求此最小值.
【答案】(1)y=﹣![]() x2+2
x2+2![]() x,(3,3
x,(3,3![]() );(2)t=3时,△OPA是直角三角形;(3)当t=
);(2)t=3时,△OPA是直角三角形;(3)当t=![]() 时,四边形ABPM的面积取最小值,最小值为
时,四边形ABPM的面积取最小值,最小值为![]()
【解析】
(1)根据点O,A的坐标,利用待定系数法可求出二次函数的解析式,再将二次函数解析式由一般式变形为顶点式,即可得出顶点B的坐标;
(2)由点B的坐标,利用待定系数法可求出直线OB的解析式,过点P作PC⊥x轴于点C,设点P的坐标为(x,![]() x),则点C的坐标为(x,0),由tan∠POC=
x),则点C的坐标为(x,0),由tan∠POC=![]() 可得出∠POC=60°,结合OA的值可找出当∠APO=90°时OP的长,由点P的运动速度为1可求出此时t的值;
可得出∠POC=60°,结合OA的值可找出当∠APO=90°时OP的长,由点P的运动速度为1可求出此时t的值;
(3)当运动时间为t时,OP=t,AM=2t,PC=![]() t,PC=
t,PC=![]() t,OM=6﹣2t,结合点P,M的运动速度可得出0≤t≤3,由S四边形ABPM=S△ABO﹣S△POM可得出四边形ABPM的面积关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
t,OM=6﹣2t,结合点P,M的运动速度可得出0≤t≤3,由S四边形ABPM=S△ABO﹣S△POM可得出四边形ABPM的面积关于t的函数关系式,再利用二次函数的性质即可解决最值问题.
解:(1)将O(0,0),A(6,0)代入y=﹣![]() x2+bx+c,得:
x2+bx+c,得:
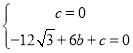 ,解得:
,解得: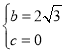 ,
,
∴该抛物线的解析式为y=﹣![]() x2+2
x2+2![]() x.
x.
∵y=﹣![]() x2+2
x2+2![]() x=﹣
x=﹣![]() (x﹣3)2+3
(x﹣3)2+3![]() ,
,
∴顶点B的坐标为(3,3![]() ).
).
(2)设直线OB的解析式为y=kx,
将B(3,3![]() )代入y=kx,得:3
)代入y=kx,得:3![]() =3k,
=3k,
解得:k=![]() ,
,
∴直线OB的解析式为y=![]() x.
x.
过点P作PC⊥x轴于点C,如图1所示.
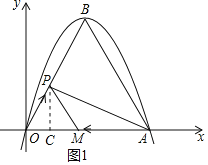
设点P的坐标为(x,![]() x),则点C的坐标为(x,0).
x),则点C的坐标为(x,0).
∵tan∠POC=![]() =
=![]() ,
,
∴∠POC=60°.
当∠APO=90°,则cos∠POC=![]() =
=![]() ,
,
∴OP=3.
∵OP=1×t=3,
∴t=3.
(3)当运动时间为t时,OP=t,AM=2t,PC=![]() t,PC=
t,PC=![]() t,OM=6﹣2t.
t,OM=6﹣2t.
∵当P、M其中一个点停止运动时另一个点也随之停止运动,
∴0≤t≤3.
S四边形ABPM=S△ABO﹣S△POM,
=![]() OAyB﹣
OAyB﹣![]() OMPC,
OMPC,
=![]() ×6×3
×6×3![]() ﹣
﹣![]() ×(6﹣2t)×
×(6﹣2t)×![]() t,
t,
=![]() t2﹣
t2﹣![]() t+9
t+9![]() ,
,
=![]() (t﹣
(t﹣![]() )2+
)2+![]() .
.
∵![]() >0,
>0,
∴当t=![]() 时,四边形ABPM的面积取最小值,最小值为
时,四边形ABPM的面积取最小值,最小值为![]() .
.

【题目】 “六一”前夕质监部门从某超市经销的儿童玩具、童车和童装中共抽查了300件儿童用品,以下是根据抽查结果绘制出的不完整的统计表和扇形图;
类别 | 儿童玩具 | 童车 | 童装 |
抽查件数 | 90 |

请根据上述统计表和扇形提供的信息,完成下列问题:
(1)分别补全上述统计表和统计图;
(2)已知所抽查的儿童玩具、童车、童装的合格率分别为90%、88%、80%,若从该超市的这三类儿童用品中随机购买一件,买到合格品的概率是多少?