题目内容
【题目】如图，已知△ABC三个顶点坐标分别是A（1，3），B（4，1），C（4，4）．
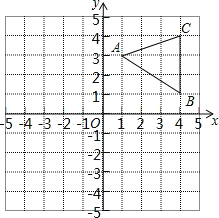
（1）请按要求画图：
①画出△ABC向左平移5个单位长度后得到的△A1B1C1；
②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2．
（2）请写出直线B1C1与直线B2C2的交点坐标．
【答案】(1)画图见解析；（2）（-1，-4）．
【解析】
试题分析：（1）①根据网格结构找出点A、B、C平移后的对应点A1、B1、C1的位置，然后顺次连接即可；②根据旋转角度，旋转方向，分别找到A、B、C的对应点，顺次连接可得△A2B2C2；
（2）由图形可知交点坐标；
试题解析：（1）①如图所示：
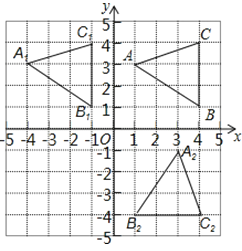
△A1B1C1即为所求；
②如图所示：△A2B2C2，即为所求；
（2）由图形可知：交点坐标为（-1，-4）．
练习册系列答案
相关题目
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（
）、面数（
）、棱数（
）之间存在的一个有趣的关系式，被称为欧拉公式，请你观察下列几种简单多面体模型，解答下列问题：
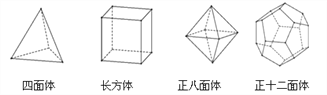
（1）根据上面多面体模型，完成表格中的空格；
多面体 | 顶点数（ | 面数（ | 棱数（ |
四面体 |
|
| |
长方体 |
|
|
|
正八面体 |
|
| |
正十二面体 |
|
|
|
（1）你发现顶点数（）、面数（）、棱数（）之间存在的关系式是_______.
（2）正十二面体有
个顶点，那它有______条棱；
（3）一个多面体的面数比顶点数大
，且有
条棱，则这多面体的顶点数是______；
（4）某个玻璃饰品的外形是简单多面体，它的外表是由三角形和八边形两种多边形拼接而成，且有
个顶点，每个顶点处都有
条棱，设该多面体表面三角形的个数为
个，八边形的个数为
个，求
的值.