Question

【题目】如图，正方形ABCD内有一点P，若PA=1，PB=2，PC=3．

(1)画出△ABP绕点B顺时针旋转90°得到的△CBE；

(2)求∠APB度数；

(3)求正方形ABCD的面积．

Answer 1

【答案】(1)画图见解析；(2)∠APB=135°；(3)正方形ABCD的面积为5+2．

【解析】

（1）作∠QBC=∠ABP，BP=BQ=2，连接QC即可得出△BCQ；

（2）先由△BPQ是等腰直角三角形求出∠BQP的度数，再证明∠PQC=90°，即可得出∠BQC的度数，进而得出结论；

（3）如图，作CH⊥BQ交BQ的延长线于H．求出BH，CH，利用勾股定理即可解决问题.

(1)作∠QBC=∠ABP，BP=BQ=2，连接QC即可得出△BCQ；

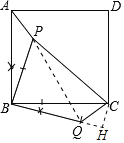
(2)连接PQ，

在Rt△PBQ中∵BP=BQ=2，

∴PQ2=BP2+BQ2=22+22=8，

在△PCQ中，

∵PC=3，QC=AP=1，

∴PC2=PQ2+QC2，

∴△PCQ是直角三角形，∠PQC=90°，

∵BP=BQ=2，∠PBQ=90°，

∴△PBQ是等腰直角三角形，

∴∠BQP=45°，

∵∠PQC=90°，

∴∠BQC=∠BQP+∠PQC=45°+90°=135°，

∵△BQC由△BPA旋转而成，

∴∠APB=∠BQC=135°．

(3)如图，作CH⊥BQ交BQ的延长线于H，

∵∠BQC=135°，

∴∠CQH=∠QCH=45°，

∴CH=QH，∵CQ=QP=1，

∴CH=QH=，

∴BH=BQ+QH=2+，

在Rt△BCH中，BC===，

∴正方形ABCD的面积为5+2．