Question

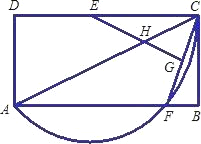
【题目】已知：如图，矩形ABCD中，点E、F分别在DC，AB边上，且点A、F、C在以点E为圆心，EC为半径的圆上，连接CF，作EG⊥CF于G，交AC于H．已知AB＝6，设BC＝x，AF＝y．

（1）求证：∠CAB＝∠CEG；

（2）①求y与x之间的函数关系式． ②x＝　 　时，点F是AB的中点；

（3）当x为何值时，点F是的中点，以A、E、C、F为顶点的四边形是何种特殊四边形？试说明理由．

Answer 1

【答案】（1）证明见解析（2）①y＝﹣x2+6②3（3）2

【解析】

（1）连接EF，由于EG经过圆心E，且与弦CF垂直，由垂径定理知∠CEF＝2∠CEG，而圆周角∠CAF和圆心角∠CEG所对的弧正好相同，由圆周角定理知∠CEG＝2∠CAF，由此得证；

（2）①设⊙O的半径为r，连接EA、EF；由于EA＝EF，那么E点在AF的垂直平分线上，因此AF＝2DE，即y＝2（6﹣r），所以只需求出r、x的关系式即可；Rt△ADE中，AD＝x，用r可表示出AE、DE的长，即可由勾股定理求得r、x的关系式，由此得解；②当F是AB中点时，AF＝y＝3，将其代入①的函数关系式中，即可求得x的值；

（3）当F是弧AC的中点时，EF垂直平分AC，可得AE＝EC，AF＝FC；易知∠AEF＝∠CEF，而∠CEF和∠AFE是平行线的内错角，等量代换后可得∠AEF＝∠AFE＝∠FAE，由此可证得△EAF是正三角形，由此可证得四边形AECF的四边都相等，即四边形AECF是菱形；此时∠CFB＝∠EAF＝60°，在Rt△CFB中，易知BF＝CF，而AF＝FC，那么BF即为AF的一半、AB的三分之一，由此可求得BF的长，进而可得到BC（即x）的长．

（1）连接EF（如图1），

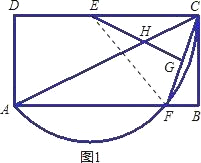
∵点A、F、C在以点E为圆心，EC为半径的圆上，

∴EF＝EC，

∵EG⊥CF，

∴∠CEF＝2∠CEG，

∵∠CEF＝2∠CAB，∴∠CAB＝∠CEG；

（2）（如图2）①连接EF、EA，

设⊙E的半径为r，

在Rt△ADE中，EA＝r，DE＝6﹣r，AD＝x，

∴x2+（6﹣r）2＝r2，r＝x2+3，

∵EF＝EA，

∴AF＝2DE，

即y＝2（6﹣r）＝﹣x2+6；

②点F是AB的中点时，y＝3，即﹣x2+6＝3，

∴x＝；

（3）（如图3）

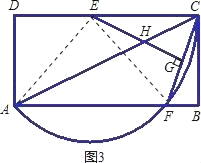
当x＝时，F是弧AC的中点．此时四边形AECF菱形；

理由如下：

∵点F是弧AC的中点，

∴∠AEF＝∠CEF，AF＝CF，

∵AB∥CD，

∴∠AFE＝∠CEF，

∴∠AEF＝∠AFE，

∴AE＝AF，

∵AE＝EF，

∴AE＝AF＝CE＝CF，

∴△AEF和△CEF都是正三角形，

∴四边形AECF是菱形，且∠CEF＝60°，

∴∠BCF＝30°，∴BF＝CF＝AF＝AB＝2，BC＝．