题目内容
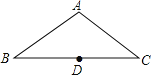
【题目】如图,在四边形ABCD中,∠BCD是钝角,AB=AD,BD平分∠ABC.若CD=3,BD=2![]() ,sin∠DBC=
,sin∠DBC=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】AC=2![]() .
.
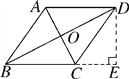
【解析】试题过点D作DE⊥BC交BC的延长线于点E,则∠E=90°,在Rt△BDE中,由sin∠DBC=![]() ,BD=2
,BD=2![]() ,可得DE、BE的长,在Rt△CDE中,由勾股定理可得CE的长,从而可得BC=CD, 再由BD平分∠ABC,可推导得到AB∥CD,同理AD∥BC,从而得到四边形ABCD是菱形,然后再利用菱形的性质及勾股定理即可求得AC的长
,可得DE、BE的长,在Rt△CDE中,由勾股定理可得CE的长,从而可得BC=CD, 再由BD平分∠ABC,可推导得到AB∥CD,同理AD∥BC,从而得到四边形ABCD是菱形,然后再利用菱形的性质及勾股定理即可求得AC的长
试题解析:BC交BC的延长线于点E,则∠E=90°,
∵在Rt△BDE中,sin∠DBC=![]() ,BD=2
,BD=2![]() ,∴DE=2
,∴DE=2![]() ,
,
∴BE=![]() =4,
=4,
∵在Rt△CDE中,CD=3,DE=2![]() ,∴CE=
,∴CE=![]() =1,
=1,
∴BC=BE-CE=3,∴BC=CD,∴∠CBD=∠CDB,
∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ABD=∠CDB,∴AB∥CD,
同理AD∥BC,∴四边形ABCD是菱形,
设AC交BD于O,则AC⊥BD,AO=CO=![]() AC,BO=DO=
AC,BO=DO=![]() BD=
BD=![]() ,
,
∴OC=![]() =
=![]() ,∴AC=2OC=2
,∴AC=2OC=2![]() .
.

练习册系列答案
相关题目