题目内容
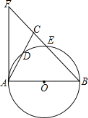
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的
为直径的![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,延长
,延长![]() 到点
到点![]() ,连接
,连接![]() ,使
,使![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】![]() 证明见解析;
证明见解析;![]() 长为
长为![]() .
.
【解析】
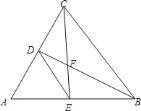
(1)连接BD,由圆周角定理得出∠ADB=90°,由等腰三角形的性质得出∠ABC=2∠ABD,得出∠ABD=∠CAF,证出∠CAF+∠CAB=90°,BA⊥FA,即可得出结论;
(2)连接AE,由圆周角定理得出∠AEB=90°,设CE长为x,则EB长为3x,AB=BC=4x.由勾股定理可得AE=![]() x,在Rt△AEC中,由勾股定理得出方程,解方程即可.
x,在Rt△AEC中,由勾股定理得出方程,解方程即可.
![]() 连接
连接![]() ,如图
,如图![]() 所示:
所示:

∵![]() 是
是![]() 的直径
的直径
∴![]() ,
,
∵![]() ,
,
∴![]() 平分
平分![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() 是
是![]() 的切线;
的切线;
![]() 连接
连接![]() ,如图
,如图![]() 所示:
所示:
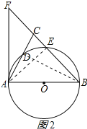
∵![]() 是
是![]() 的直径
的直径
∴![]() ,即
,即![]() 为直角三角形,
为直角三角形,
∵![]() ,
,
设![]() 长为
长为![]() ,则
,则![]() 长为
长为![]() ,
,![]() 长为
长为![]() .
.
则![]() 长为
长为![]() ,
,
在![]() 中由勾股定理可得
中由勾股定理可得![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得:![]() ,
,
解得:![]() ,
,
∵![]()
∴![]() ,即
,即![]() 长为
长为![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目