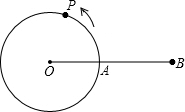
题目内容
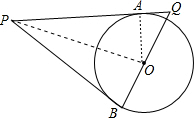
如图，P是⊙O外一点，PA是⊙O的切线，A是切点，B是⊙O上一点，且PA=PB，连接BO并延长与切线PA相交于点Q．求证：
（1）PB是⊙O的切线；
（2）AQ•PQ=OQ•BQ．
（1）PB是⊙O的切线；
（2）AQ•PQ=OQ•BQ．
证明：（1）连结OA、OP，如图，
∵PA是⊙O的切线，
∴OA⊥PA，
∴∠OAP=90°，
在△PAO和△PBO中，
，
∴△PAO≌△PBO（SSS），
∴∠OBP=∠OAP=90°，
∴OB⊥PB，
∴PB是⊙O的切线；
（2）∵∠OBP=∠OAP=90°，
而∠AQO=∠BQP，
∴Rt△PBQ∽Rt△OAQ，
∴PQ：OQ=BQ：AQ，
∴AQ•PQ=OQ•BQ．
∵PA是⊙O的切线，
∴OA⊥PA，
∴∠OAP=90°，
在△PAO和△PBO中，
|
∴△PAO≌△PBO（SSS），
∴∠OBP=∠OAP=90°，
∴OB⊥PB，
∴PB是⊙O的切线；
（2）∵∠OBP=∠OAP=90°，
而∠AQO=∠BQP，
∴Rt△PBQ∽Rt△OAQ，
∴PQ：OQ=BQ：AQ，
∴AQ•PQ=OQ•BQ．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
