题目内容
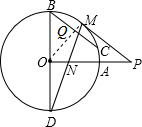
如图，BD是⊙O的直径，OA⊥OB，M是劣弧AB上的一点，过点M作⊙O的切线MP交OA的延长线于点P，MD与OA交于点N．
（1）求证：PM=PN；
（2）若BC=3，PA=
BO，过点B作BC∥MP交⊙O于点C，求BO的长．
（1）求证：PM=PN；
（2）若BC=3，PA=
| 3 |
| 5 |
（1）证明：连接OM交BC于点Q，
∵PM是⊙O的切线，
∴OM⊥MP，
即∠OMP=90°，
∴∠PMN=90°-∠OMD，
∵∠PNM=∠OND=90°-∠ODM，
∵OD=OM，
∴∠OMD=∠ODM，
∴∠PMN=∠PNM，
∴PM=PN；
（2）由（1）∠OMP=90°，
∵MP∥BC，
∴OM⊥BC，BC=3，
∴BQ=
，
∵∠BOM+∠MOP=90°，∠P+∠MOP=90°，
∴∠BOM=∠P，
∴sin∠BOQ=sin∠P，
∴
=
，
∵OB=OM=OA，
∴OP=OA+
BO=
BO，
∴
=
，
∴OB=
．
∵PM是⊙O的切线，
∴OM⊥MP，
即∠OMP=90°，
∴∠PMN=90°-∠OMD，
∵∠PNM=∠OND=90°-∠ODM，
∵OD=OM，
∴∠OMD=∠ODM，
∴∠PMN=∠PNM，
∴PM=PN；
（2）由（1）∠OMP=90°，
∵MP∥BC，
∴OM⊥BC，BC=3，
∴BQ=
| 3 |
| 2 |
∵∠BOM+∠MOP=90°，∠P+∠MOP=90°，
∴∠BOM=∠P，
∴sin∠BOQ=sin∠P，
∴
| BQ |
| BO |
| OM |
| OP |
∵OB=OM=OA，
∴OP=OA+
| 3 |
| 5 |
| 8 |
| 5 |
∴
| ||
| BO |
| OB | ||
|
∴OB=
| 12 |
| 5 |
练习册系列答案
相关题目
