题目内容
【题目】如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E,F分别是AC,BC的中点,直线EF与⊙O交于G,H两点,若⊙O的半径为6,则GE+FH的最大值为( )
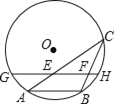
A. 6 B. 9 C. 10 D. 12
【答案】B
【解析】
首先连接OA、OB,根据圆周角定理,求出∠AOB=2∠ACB=60°,进而判断出△AOB为等边三角形;然后根据⊙O的半径为6,可得AB=OA=OB=6,再根据三角形的中位线定理,求出EF的长度;最后判断出当弦GH是圆的直径时,它的值最大,进而求出GE+FH的最大值是多少即可.
解:如图,连接OA、OB,
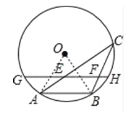 ,
,
∵∠ACB=30°,
∴∠AOB=2∠ACB=60°,
∵OA=OB,
∴△AOB为等边三角形,
∵⊙O的半径为6,
∴AB=OA=OB=6,
∵点E,F分别是AC、BC的中点,
∴EF=![]() AB=3,
AB=3,
要求GE+FH的最大值,即求GE+FH+EF(弦GH)的最大值,
∵当弦GH是圆的直径时,它的最大值为:6×2=12,
∴GE+FH的最大值为:12﹣3=9.
故选:B.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
【题目】某校为了解九年级![]() 名学生的体育综合素质,随机抽查了
名学生的体育综合素质,随机抽查了![]() 名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图。
名学生进行体育综合测试,所得成绩整理分成五组,并制成如下频数分布表和扇形统计图。
频数分布表:
组别 | 成绩(分) | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

请你根据以上图表提供的信息,解答下列问题:
(1)频数分布表中的![]() ;
;![]()
(2)扇形统计图中,![]() 组所对应的扇形圆心角的度数是_ 度.
组所对应的扇形圆心角的度数是_ 度.