题目内容
【题目】随着人们生活质量的提高,越来越多的人们关注运动与健康,近来“微信运动”逐渐被大家关注和喜爱.某兴趣小组为了了解某社区居民的“微信运动”情况,进行了随机抽样调查,对他们一日“微信运动”中的步数进行了统计,下面给出部分信息:
①
| 频数 | 频率 |
| 5 |
|
| 10 | 0.2 |
| 15 | 0.3 |
|
| 0.2 |
| 8 | 0.16 |
| 2 | 0.04 |
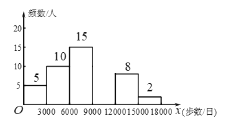
![]() 这一组的数据为:
这一组的数据为:
6000 6200 6200 6500 6600 6800 7000 7200 7200 7200 7800 8000 8300 8700 8900
根据以上信息,回答下列问题:
(1)本次被调查的居民有__________人:表中![]() ______________,
______________,![]() ___________;
___________;
(2)补全频数分布直方图;
(3)直接写出被调查的居民在“微信运动”中步数的中位数;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数.
【答案】(1)50,a=0.1,b=10 (2)补全图形见解析,(3)7500;(4)2000人.
【解析】
(1)根据频率=频数÷总数这一数量关系,即可得出答案;
(2)根据(1)中b的数值,补全步数在![]() 的部分即可;
的部分即可;
(3)根据中位数的定义进行观察计算即可求解;
(4)用样本中超过9000步(包含9000步)的频率之和乘以总人数5000可得答案.
解:(1)根据频率=频数÷总数,
本次调查的居民人数为:![]() 人,
人,
![]() ,
,
![]() ,
,
∴本次调查的居民总人数为50人,表中![]() ,
,![]() ;
;
(2)频数分布直方图如图所示,
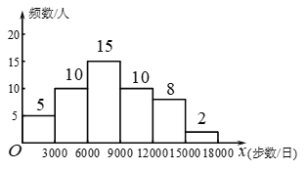
(3)∵被调查居民人数为50人,
∴被调查的居民在“微信运动”中步数的中位数为(步数排名第25位的步数+步数排名第26位的步数)÷2,
即,![]() 步,
步,
故答案为:7500;
(4)本社区约有5000人,用调查样本估计一日步数不低于9000步的人数为,![]() 人,
人,
答:该社区一日步数不低于9000步的人数为2000人.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案【题目】某公司为了宣传一种新产品,在某地先后举行![]() 场产品促销会,已知该产品每台成本为
场产品促销会,已知该产品每台成本为![]() 万元,设第
万元,设第![]() 场产品的销售量为
场产品的销售量为![]() (台),在销售过程中获得以下信息:
(台),在销售过程中获得以下信息:
信息1:已知第一场销售产品![]() 台,然后每增加一场,产品就少卖出
台,然后每增加一场,产品就少卖出![]() 台;
台;
信息2:产品的每场销售单价![]() (万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次
(万元)由基本价和浮动价两部分组成,其中基本价保持不变,第1场--第20场浮动价与销售场次![]() 成正比,第21场--第40场浮动价与销售场次
成正比,第21场--第40场浮动价与销售场次![]() 成反比,经过统计,得到如下数据:
成反比,经过统计,得到如下数据:
| 3 | 10 | 25 |
| 10.6 | 12 | 14.2 |
(1)求![]() 与
与![]() 之间满足的函数关系式;
之间满足的函数关系式;
(2)当产品销售单价为13万元时,求销售场次是第几场?
(3)在这![]() 场产品促销会中,哪一场获得的利润最大,最大利润是多少?
场产品促销会中,哪一场获得的利润最大,最大利润是多少?
【题目】某校九年级( 3 )班全体学生 2019 年初中毕业体育考试的成绩统计如下表:
成绩 | 35 | 39 | 42 | 43 | 45 | 49 | 50 |
人数 | 3 | 5 | 6 | 6 | 8 | 7 | 5 |
根据上表中的信息判断,下列结论中错误的是 ( )
A.该班一共有 40 名同学B.该班学生这次考试成绩的众数是 45 分
C.该班学生这次考试成绩的中位数是 44 分D.该班学生这次考试成绩的平均数是 45 分