题目内容
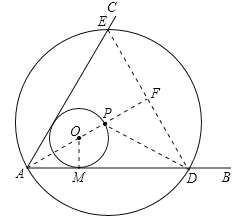
【题目】如图∠BAC=60°,半径长1的⊙O与∠BAC的两边相切,P为⊙O上一动点,以P为圆心,PA长为半径的⊙P交射线AB、AC于D、E两点,连接DE,则线段DE长度的最大值为( )

A. 3 B. 6 C. ![]() D.
D. ![]()
【答案】D
【解析】
连接AO并延长,与圆O交于P点,当AF垂直于ED时,线段DE长最大,设圆O与AB相切于点M,连接OM,PD,由对称性得到AF为角平分线,得到∠FAD为30度,根据切线的性质得到OM垂直于AD,在直角三角形AOM中,利用30度角所对的直角边等于斜边的一半求出AO的长,由AO+OP求出AP的长,即为圆P的半径,由三角形AED为等边三角形,得到DP为角平分线,在直角三角形PFD中,利用30度所对的直角边等于斜边的一半求出PF的长,再利用勾股定理求出FD的长,由DE=2FD求出DE的长,即为DE的最大值.
连接AO并延长,与ED交于F点,与圆O交于P点,此时线段ED最大,连接OM,PD,可得F为ED的中点.
∵∠BAC=60°,AE=AD,∴△AED为等边三角形,∴AF为角平分线,即∠FAD=30°.在Rt△AOM中,OM=1,∠OAM=30°,∴OA=2,∴PD=PA=AO+OP=3.在Rt△PDF中,∠FDP=30°,PD=3,∴PF=![]() ,根据勾股定理得:FD=
,根据勾股定理得:FD=![]() =
=![]() ,则DE=2FD=3
,则DE=2FD=3![]() .
.
故选D.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目