题目内容
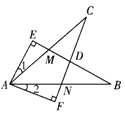
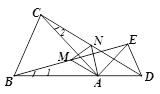
【题目】已知:如图所示,在ΔABC和ΔADE中,AB=AC,AD=AE,∠BAC=∠DAE,,且点B,A,D在同一条直线上,连接BE,CD,M,N分别为BE,CD的中点, 连接AM,AN,MN.
⑴.求证:BE=CD
⑵.求证:ΔAMN是等腰三角形.

【答案】(1)证明见解析;(2)证明见解析;
【解析】试题分析:(1)由∠BAC=∠DAE,等式左右两边都加上∠CAE,得到一对角相等,再由AB=AC,AF为公共边,利用SAS可得出三角形ABE与三角形ACD全等,由全等三角形的对应边相等可得出BE=CD;
(2)由M与N分别为BE,CD的中点,且BE=CD,可得出ME=ND,由三角形ABE与三角形ACD全等,得到对应边AE=AD,对应角∠AEB=∠ADC,利用SAS可得出三角形AME与三角形AND全等,利用全等三角形的对应边相等可得出AM=AN,即三角形AMN为等腰三角形.
试题解析:⑴.∵![]()
∴![]()
即![]()
在![]() 和
和![]() 中
中
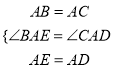
∴![]() ≌
≌![]()
∴![]()
⑵.由![]() ≌
≌![]() 知:
知: ![]()
又∵![]() 分别为
分别为![]() 的中点,且
的中点,且![]()
∴![]()
在![]() 和
和![]() 中
中
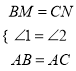
∴![]() ≌
≌![]()
∴![]() 即
即![]() 是等腰三角形
是等腰三角形

练习册系列答案
相关题目