题目内容
【题目】如图,在△ABC中,∠ACB=3∠B,AB=10,AC=4,AD平分∠BAC,交BC于点D,CE⊥AD于E,则CE= ______.

【答案】3
【解析】
作辅助线来构造全等三角形,将已知边长AC和AB之间建立联系,求得AF、BF,再利用∠ACB和∠B之间的关系求出CF,从而得到CE的长.
延长CE交AB于F,
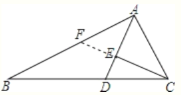
∵CE⊥AD,
∴∠AEF=∠AEC=90°,
∵AD平分∠BAC,
∴∠FAE=∠CAE,
在△AEF与△ACE中,
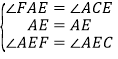
∴△AEF≌△ACE,
∴AF=AC=4,∠AFE=∠ACE,EF=CE,
∴BF=10-4=6,
∵∠AFC=∠B+∠ECD,
∴∠ACF=∠B+∠ECD,
∴∠ACB=2∠ECD+∠B,
∵∠ACB=3∠B,
∴2∠ECD+∠B=3∠B,
∴∠B=∠ECD,
∴CF=BF=6,
∴CE=![]() CF=3.
CF=3.
故答案为:3.

练习册系列答案
相关题目