题目内容
已知:如图,⊙O的半径OC垂直弦AB于点H,连接BC,过点A作弦AE∥BC,过点C作CD∥BA交 EA延长线于点D,延长CO交AE于点F.
EA延长线于点D,延长CO交AE于点F.
(1)求证:CD为⊙O的切线;
(2)若BC=5,AB=8,求OF的长.
 EA延长线于点D,延长CO交AE于点F.
EA延长线于点D,延长CO交AE于点F.(1)求证:CD为⊙O的切线;
(2)若BC=5,AB=8,求OF的长.
(1)证明:∵OC⊥AB,CD∥BA,
∴∠DCF=∠AHF=90°,
∴CD为⊙O的切线.
(2)∵OC⊥AB,AB=8,
∴AH=BH=
=4,
在Rt△BCH中,∵BH=4,BC=5,
由勾股定理得:CH=3,
∵AE∥BC,
∴∠B=∠HAF,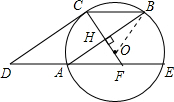
∵∠BHC=∠AHF,BH=AH,
∴△HAF≌△HBC,
∴FH=CH=3,CF=6,
连接BO,设BO=x,则OC=x,OH=x-3.
在Rt△BHO中,由勾股定理得:42+(x-3)2=x2,
解得x=
,
∴OF=CF-OC=
,
答:OF的长是
.
∴∠DCF=∠AHF=90°,
∴CD为⊙O的切线.
(2)∵OC⊥AB,AB=8,
∴AH=BH=
| AB |
| 2 |
在Rt△BCH中,∵BH=4,BC=5,
由勾股定理得:CH=3,
∵AE∥BC,
∴∠B=∠HAF,

∵∠BHC=∠AHF,BH=AH,
∴△HAF≌△HBC,
∴FH=CH=3,CF=6,
连接BO,设BO=x,则OC=x,OH=x-3.
在Rt△BHO中,由勾股定理得:42+(x-3)2=x2,
解得x=
| 25 |
| 6 |
∴OF=CF-OC=
| 11 |
| 6 |
答:OF的长是
| 11 |
| 6 |

练习册系列答案
相关题目

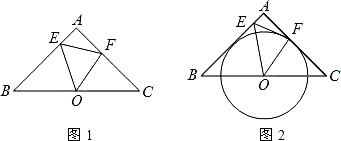




 点E作EF⊥AB于点F.建立如图所示的平面直角坐标系,已知A、B两点坐标分别为A(2,0)、B(0,
点E作EF⊥AB于点F.建立如图所示的平面直角坐标系,已知A、B两点坐标分别为A(2,0)、B(0,