Question

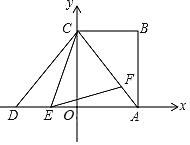
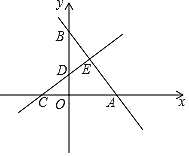
【题目】如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、点B，直线CD与x轴、y轴分别交于点C、点D，AB与CD相交于点E，线段OA、OC的长是一元二次方程x2﹣18x+72＝0的两根（OA＞OC），BE＝5，OB=OA．

(1)求点A、点C的坐标；

(2)求直线CD的解析式；

(3)在x轴上是否存在点P，使点C、点E、点P为顶点的三角形与△DCO相似？若存在，请求出点P的坐标；如不存在，请说明理由．

Answer 1

【答案】（1）A（12，0）；C（﹣6，0）；（2）y＝﹣x+8；（3）存在；P的坐标是（19，0）和（3，0）．

【解析】

（1）首先解方程x2-18x+72=0求得方程的根，则A和C的坐标即可求得；

（2）根据三角函数求得B的坐标，作EF⊥x轴于点F，根据△AEF∽△ABO，利用相似三角形的性质求得EF和OF的长，即可求得E的坐标利用待定系数法确定函数关系式；

（3）设P的坐标是（p，0），则PC=p+6．分成△COD∽△CEP和△COD∽△CPE两种情况进行讨论即可求解．

解：（1）x2﹣18x+72＝0即（x﹣12）（x﹣6）＝0，

则x﹣12＝0，x﹣6＝0，

解得：x＝12或x＝6，

又∵OA＞OC，

∴OA＝12，OC＝6，

∴A的坐标是（12，0），C的坐标是（﹣6，0）．

（2）∵,

∴,

则B的坐标是（0，16）．

作EF⊥x轴于点F．

则△AEF∽△ABO，

∴,

∴

∴AF＝9，EF＝12，

则OF＝12﹣9＝3，

则E的坐标是（3，12）．

设直线CD的解析式是y＝kx+b，则

解得：,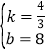

则直线CD的解析式是y＝x+8；

（3）设P的坐标是（p，0），则PC＝p+6．

当△COD∽△CEP时，，即，

解得：d＝19，

则P的坐标是（19，0）；

当△COD∽△CPE时，，则,

解得：p＝3，

则P的坐标是（3，0）

总之，P的坐标是（19，0）和（3，0）．