题目内容
【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)①如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;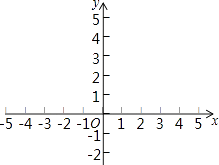
(3)该函数的最小值为;
(4)已知直线 ![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
【答案】
(1)1,﹣10
(2)该函数的图象如图
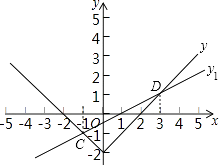
根据函数图象可得:
(3)-2
(4)﹣1≤x≤3
【解析】解:(1)①把x=3代入y=|x|﹣2,得m=3﹣2=1.
所以答案是1;②把y=8代入y=|x|﹣2,得8=|x|﹣2,
解得x=﹣10或10,
∵A(n,8),B(10,8)为该函数图象上不同的两点,
∴n=﹣10.
所以答案是﹣10;
⑵在同一平面直角坐标系中画出函数 ![]() 与函数y=|x|﹣2的图象,
与函数y=|x|﹣2的图象,
⑶该函数的图象如图,①该函数的最小值为﹣2;

所以答案是:(1)①1;②-10;(2)见解答过程;(3)﹣2;⑷﹣1≤x≤3.
【考点精析】根据题目的已知条件,利用一次函数的性质和一次函数的图象和性质的相关知识可以得到问题的答案,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

 阅读快车系列答案
阅读快车系列答案【题目】五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
类别 | 电视机 | 洗衣机 |
进价(元/台) | 1800 | 1500 |
售价(元/台) | 2000 | 1600 |
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价﹣进价)