题目内容
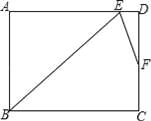
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)
【答案】6![]() +3
+3
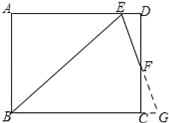
【解析】试题分析:先延长EF和BC,交于点G,再根据条件可以判断三角形ABE为等腰直角三角形,并求得其斜边BE的长,然后根据条件判断三角形BEG为等腰三角形,最后根据△EFD∽△GFC得出CG与DE的倍数关系,并根据BG=BC+CG进行计算即可.延长EF和BC,交于点G
∵矩形ABCD中,∠B的角平分线BE与AD交于点E,∴∠ABE=∠AEB=45°,∴AB=AE=9,
∴直角三角形ABE中,BE=![]() =
=![]() ,又∵∠BED的角平分线EF与DC交于点F,∴∠BEG=∠DEF
,又∵∠BED的角平分线EF与DC交于点F,∴∠BEG=∠DEF
∵AD∥BC∴∠G=∠DEF∴∠BEG=∠G∴BG=BE=![]()
由∠G=∠DEF,∠EFD=∠GFC,可得△EFD∽△GFC∴![]()
设CG=x,DE=2x,则AD=9+2x=BC ∵BG=BC+CG ∴![]() =9+2x+x 解得x=
=9+2x+x 解得x=![]()
∴BC=9+2(﹣3)=![]()

【题目】为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分
分组 | 家庭用水量x/吨 | 家庭数/户 |
A | 0≤x≤4.0 | 4 |
B | 4.0<x≤6.5 | 13 |
C | 6.5<x≤9.0 | |
D | 9.0<x≤11.5 | |
E | 11.5<x≤14.0 | 6 |
F | x>4.0 | 3 |
根据以上信息,解答下列问题
(1)家庭用水量在4.0<x≤6.5范围内的家庭有 户,在6.5<x≤9.0范围内的家庭数占被调查家庭数的百分比是 %;
(2)本次调查的家庭数为 户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是 %;
(3)家庭用水量的中位数落在 组;
(4)若该小区共有200户家庭,请估计该月用水量不超过9.0吨的家庭数.
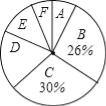
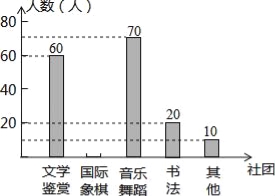
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
所占百分比 | a | 20% | b | 10% | 5% |
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.