题目内容
【题目】五一节期间，电器市场火爆，某商店需要购进一批电视机和洗衣机，根据市场调查，电视机与洗衣机的进价和售价如下表：
类别 | 电视机 | 洗衣机 |
进价（元/台） | 1800 | 1500 |
售价（元/台） | 2000 | 1600 |
若该商店计划电视机和洗衣机共100台，设购进电视机x台，获得的总利润y元．
（1）求出y与x的函数关系；
（2）已知商店最多筹集资金161800元，求购进多少台电视机，才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多？并求出最多利润．（利润=售价﹣进价）
【答案】
（1）解：y=（2000﹣1800）x+（1600﹣1500）（100﹣x）=100x+10000
（2）解：依题意得，1800x+1500（100﹣x）≤161800，
解得，x≤39 
，
∵x是整数，
∴x的最大值是39．
∵y=100x+10000中，k=100＞0，
∴y随x的增大而增大，
∴当x=39时，y有最大值，最大值是：100×39+10000=13900（元）．
【解析】（1）根据总利润=一台电视机的利润×电视机的销售量+一台洗衣机的利润×洗衣机的销售量列出解析式即可；
（2）首先依据商店最多筹集资金161800元列出不等式，然后求得不等式的解集，最后，再根据一次函数的性质可得到获利最多的方案.
【题目】问题：探究函数y=|x|﹣2的图象与性质．
小华根据学习函数的经验，对函数y=|x|﹣2的图象与性质进行了探究．
下面是小华的探究过程，请补充完整：
（1）在函数y=|x|﹣2中，自变量x可以是任意实数；
如表是y与x的几组对应值．
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=；
②若A（n，8），B（10，8）为该函数图象上不同的两点，则n=；
（2）①如图，在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点．并根据描出的点，画出该函数的图象；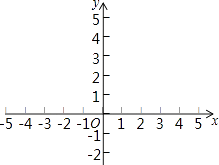
（3）该函数的最小值为；
（4）已知直线 
与函数y=|x|﹣2的图象交于C、D两点，当y1≥y时x的取值范围是 ．