题目内容
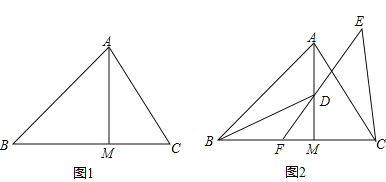
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 .
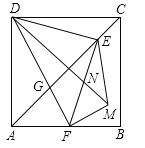
【答案】![]() .
.
【解析】
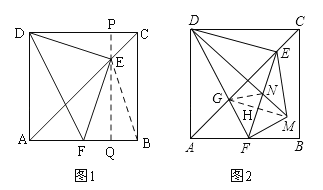
试题分析:如图1,过E作PQ⊥DC,交DC于P,交AB于Q,连接BE,∵DC∥AB,∴PQ⊥AB,∵四边形ABCD是正方形,∴∠ACD=45°,∴△PEC是等腰直角三角形,∴PE=PC,设PC=x,则PE=x,PD=4﹣x,EQ=4﹣x,∴PD=EQ,∵∠DPE=∠EQF=90°,∠PED=∠EFQ,∴△DPE≌△EQF,∴DE=EF,易证明△DEC≌△BEC,∴DE=BE,∴EF=BE,∵EQ⊥FB,∴FQ=BQ=![]() BF,∵AB=4,F是AB的中点,∴BF=2,∴FQ=BQ=PE=1,∴CE=
BF,∵AB=4,F是AB的中点,∴BF=2,∴FQ=BQ=PE=1,∴CE=![]() ,Rt△DAF中,DF=
,Rt△DAF中,DF=![]() =
=![]() ,∵DE=EF,DE⊥EF,∴△DEF是等腰直角三角形,∴DE=EF=
,∵DE=EF,DE⊥EF,∴△DEF是等腰直角三角形,∴DE=EF=![]() =
=![]() ,∴PD=
,∴PD=![]() =3,如图2,∵DC∥AB,∴△DGC∽△FGA,∴
=3,如图2,∵DC∥AB,∴△DGC∽△FGA,∴![]() =
=![]() =2,∴CG=2AG,DG=2FG,∴FG=
=2,∴CG=2AG,DG=2FG,∴FG=![]() =
=![]() ,∵AC=
,∵AC=![]() =
=![]() ,∴CG=
,∴CG=![]() =
=![]() ,∴EG=
,∴EG=![]() =
=![]() ,连接GM、GN,交EF于H,∵∠GFE=45°,∴△GHF是等腰直角三角形,∴GH=FH=
,连接GM、GN,交EF于H,∵∠GFE=45°,∴△GHF是等腰直角三角形,∴GH=FH=![]() =
=![]() ,∴EH=EF﹣FH=
,∴EH=EF﹣FH=![]() ﹣
﹣![]() =
=![]() ,∴∠NDE=∠AEF,∴tan∠NDE=tan∠AEF=
,∴∠NDE=∠AEF,∴tan∠NDE=tan∠AEF=![]() ,∴
,∴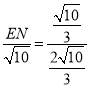 =
=![]() ,∴EN=
,∴EN=![]() ,∴NH=EH﹣EN=
,∴NH=EH﹣EN=![]() ﹣
﹣![]() =
=![]() ,Rt△GNH中,GN=
,Rt△GNH中,GN=![]() =
=![]() =
=![]() ,由折叠得:MN=GN,EM=EG,∴△EMN的周长=EN+MN+EM=
,由折叠得:MN=GN,EM=EG,∴△EMN的周长=EN+MN+EM=![]() +
+![]() +
+![]() =
=![]() ;
;
故答案为:![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案【题目】问题:探究函数y=|x|﹣2的图象与性质.
小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.
下面是小华的探究过程,请补充完整:
(1)在函数y=|x|﹣2中,自变量x可以是任意实数;
如表是y与x的几组对应值.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 1 | 0 | ﹣1 | ﹣2 | ﹣1 | 0 | m | … |
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)①如图,在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;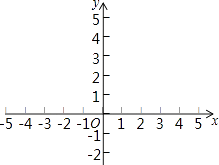
(3)该函数的最小值为;
(4)已知直线 ![]() 与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .
与函数y=|x|﹣2的图象交于C、D两点,当y1≥y时x的取值范围是 .