题目内容
【题目】将下列推理过程填写完整. 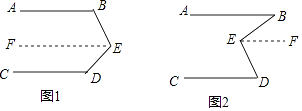
(1)如图1,已知∠B+∠BED+∠D=360°,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D+∠DEF=180°,()
∵∠B+∠BED+∠D=360°,(已知)
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF)=360°﹣180°=180°
∴EF∥AB,()
∴∥ , (平行于同一直线的两直线平行)
(2)如图2,已知∠BED=∠B+∠D,求证AB∥CD. 证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,()
∵∠BED=∠B+∠D(已知)
∴∠B=∠BEF﹣∠D=∠BED﹣∠FED=∠BEF,
∴∥ , ()
∴∥ . (平行于同一直线的两直线平行)
【答案】
(1)两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD
(2)两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【解析】(1.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行) ∵EF∥CD,
∴∠D+∠DEF=180°,( 两直线平行,同旁内角互补 )
∵∠B+∠BED+∠D=360°,( 已知 )
∴∠B+∠BEF=∠B+∠BED+∠D﹣(∠D+∠DEF )=360°﹣180°=180°,
∴EF∥AB,( 同旁内角互补,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行);
所以答案是:两直线平行,同旁内角互补;同旁内角互补,两直线平行;AB;CD;
(2.)证明:过E点作EF∥CD(过直线外一点有且只有一条直线与已知直线平行)
∵EF∥CD,
∴∠D=∠FED,( 两直线平行,内错角相等 )
∵∠BED=∠B+∠D,(已知)
∴∠B=∠BED﹣∠D=∠BED﹣∠FED=∠BEF,
∴AB∥EF,( 内错角相等,两直线平行 )
∴AB∥CD,( 平行于同一直线的两直线平行).
所以答案是:两直线平行,内错角相等;AB;EF;内错角相等,两直线平行;AB;CD.
【考点精析】通过灵活运用平行公理和平行线的判定,掌握平行公理――平行线的存在性与惟一性;经过直线外一点,有且只有一条直线与这条直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案