Question

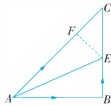
【题目】如图，在Rt△ABC的场地上，∠B＝90°，AB＝BC，∠CAB的平分线AE交BC于点E.甲、乙两人同时从A处出发，以相同的速度分别沿AC和A→B→E线路前进，甲的目的地为C，乙的目的地为E.请你判断一下，甲、乙两人谁先到达各自的目的地？并说明理由．

Answer 1

【答案】同时到达

【解析】试题分析：

由题意可知：这里是要比较AB+BE与AC的大小关系.

如图，过点E作EF⊥AC于点F，则由角平分线的性质可得BE=EF，证△EFC是等腰直角三角形可得EF=EC，从而可得BE=FC；再证△ABE≌△AFE可得AB=AF，从而可得AB+BE=AC，说明甲、乙二人会同时达到目的地.

试题解析：

甲、乙会同时到达目的地．理由如下：

过点E作EF⊥AC于点F，∵AE平分∠CAB，∠B=90°，

∴EF＝EB，∠CAE=∠BAE，

∵AB＝BC，∠B＝90°，

∴∠C＝.

∵EF⊥AC，

∴∠EFC＝90°，

∴∠CEF＝90°－∠C＝45°＝∠C，

∴EF＝CF.

∴BE=CF，

在△AEF和△AEB中， ,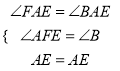

∴△AEF≌△AEB，

∴AF＝AB，

∴AB＋BE＝AF＋CF＝AC，故甲、乙同时到达目的地．