题目内容
【题目】如图1,在正方形ABCD中,E,F分别是AD,CD上两点,BE交AF于点G,且DE=CF.
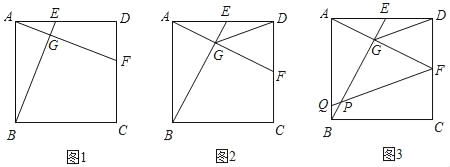
(1)写出BE与AF之间的关系,并证明你的结论;
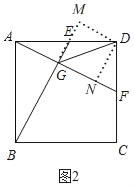
(2)如图2,若AB=2,点E为AD的中点,连接GD,试证明GD是∠EGF的角平分线,并求出GD的长;
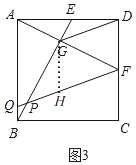
(3)如图3,在(2)的条件下,作FQ∥DG交AB于点Q,请直接写出FQ的长.
【答案】(1)BE=AF,BE⊥AF;(2)GD是∠EGF的角平分线,证明见解析,GD=![]() ;(3)FQ=
;(3)FQ=![]() .
.
【解析】
(1)根据已知条件可先证明△BAE≌△ADF,得到BE=AF,再由角的关系得到∠AGE=90°从而证明BE⊥AF;
(2)过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,根据勾股定理和三角形的面积相等求出DN,然后证明△AEG≌△DEM,得到DN=DM,再根据角平分线的性质可证明GD平分∠EGF,进而在等腰直角三角形中求得GD;
(3)过点G作GH∥AQ交FQ于H,可得到四边形DFHG是平行四边形,进而可得△FGH∽△FAQ,然后根据三角形相似的性质可求得FQ.
解:(1)BE=AF,BE⊥AF,理由:
四边形ABCD是正方形,
∴BA=AD=CD,∠BAE=∠D=90°,
∵DE=CF,
∴AE=DF,
∴△BAE≌△ADF(SAS),
∴BE=AF,∠ABE=∠DAF,
∵∠ABE+∠AEB=90°,
∴∠DAF+∠AEB=90°,
∴∠AGE=90°,
∴BE⊥AF
(2)如图2,过点D作DN⊥AF于N,DM⊥BE交BE的延长线于M,
在Rt△ADF中,根据勾股定理得,AF=![]() ,
,
∵S△ADF=![]() AD×FD=
AD×FD=![]() AF×DN,
AF×DN,
∴DN=![]() ,
,
∵△BAE≌△ADF,
∴S△BAE=S△ADF,
∵BE=AF,
∴AG=DN,
∵AE=DE,∠MED=∠AEG,∠DME=∠AGM,
∴△AEG≌△DEM(AAS),
∴AG=DM,
∴DN=DM,
∵DM⊥BE,DN⊥AF,
∴GD平分∠MGN,即GD平分∠EGF,
∴∠DGN=![]() ∠MGN=45°,
∠MGN=45°,
∴△DGN是等腰直角三角形,
∴GD=![]() DN=
DN=![]() ;
;
(3)如图3,由(2)知,GD=![]() ,AF=
,AF=![]() ,AG=DN=
,AG=DN=![]() ,
,
∴FG=AF﹣AG=![]() ,
,
过点G作GH∥AQ交FQ于H,
∴GH∥DF,
∵FQ∥DG,
∴四边形DFHG是平行四边形,
∴FH=DG=![]() ,
,
∵GH∥AQ,
∴△FGH∽△FAQ,
∴![]() ,
,
∴![]() ,
,
∴FQ=![]() .
.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案【题目】某校为更好的开展“冬季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳长绳、踢毽子、背夹球、拔河共四类),并将统计结果绘制成如图不完整的频数分布表.
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型 | 频数 | 频率 |
跳长绳 | 25 | a |
踢毽子 | 20 | 0.2 |
背夹球 | b | 0.4 |
拔河 | 15 | 0.15 |
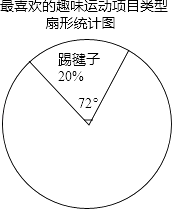
(1)直接写出a= , b=;
(2)利用频数分布表中的数据,在图中绘制扇形统计图(注明项目、百分比、圆心角);
(3)若全校共有学生1200名,估计该校最喜爱背夹球和拔河的学生大约有多少人?