Question

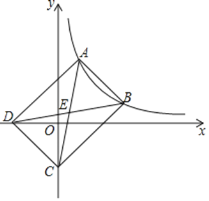
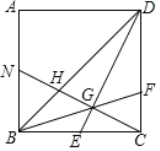
【题目】如图：四边形ABCD中，E、F、G、H分别为各边的中点，顺次连接E、F、G、H，把四边形EFGH称为中点四边形．连接AC、BD，容易证明：中点四边形EFGH一定是平行四边形．

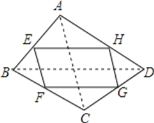
（1）如果改变原四边形ABCD的形状，那么中点四边形的形状也随之改变，通过探索可以发现：当四边形ABCD的对角线满足AC＝BD时，四边形EFGH为菱形．当四边形ABCD的对角线满足　 　时，四边形EFGH为矩形；当四边形ABCD的对角线满足　 　时，四边形EFGH为正方形；

（2）探索三角形AEH、三角形CFG与四边形ABCD的面积之间的等量关系，请写出你发现的结论，并加以证明；

（3）如果四边形ABCD的面积为2，那么中点四边形EFGH的面积是多少？

Answer 1

【答案】（1）AC⊥BD，AC⊥BD且 AC＝BD；（2）S△AEH+S△CFG＝S四边形ABCD，见解析；（3）1

【解析】

（1）若四边形EFGH为矩形，则应有EF∥HG∥AC，EH∥FG∥BD，EF⊥EH，故应有AC⊥BD；若四边形EFGH为正方形，同上应有AC⊥BD，又应有EH=EF，而EF=AC，EH=BD，故应有AC=BD．
（2）由相似三角形的面积比等于相似比的平方求解．（3）由（2）可得SEFGH=S四边形ABCD=1

解：（1）若四边形EFGH为矩形，则应有EF∥HG∥AC，EH∥FG∥BD，EF⊥EH，故应有AC⊥BD；

若四边形EFGH为正方形，同上应有AC⊥BD，又应有EH＝EF，而EF＝AC，EH＝BD，故应有AC＝BD．

（2）S△AEH+S△CFG＝S四边形ABCD．

证明：在△ABD中，

∵EH＝BD，

∴△AEH∽△ABD．

∴．

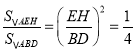即S△AEH＝S△ABD

同理可证：S△CFG＝S△CBD

∴S△AEH+S△CFG＝（S△ABD+S△CBD）＝S四边形ABCD．

（3）由（2）可知S△AEH+S△CFG＝（S△ABD+S△CBD）＝S四边形ABCD，

同理可得S△BEF+S△DHG＝（S△ABC+S△CDA）＝S四边形ABCD，

故SEFGH＝S四边形ABCD＝1．