题目内容
【题目】在平面直角坐标系中，点O为坐标原点，已知△OAB是等腰直角三角形，且∠OAB＝90°，若点A的坐标（3，1），则点B的坐标为______．
【答案】（2，4）或（4，﹣2）
【解析】
分两种情况讨论：当点B在第一象限时，过A作AC⊥x轴于C，过B作BD⊥AC于D；当点B'在第四象限时，过A作AE⊥y轴于E，过B'作B'F⊥AE于F，分别依据全等三角形的对应边相等，即可得到点B的坐标．
如图，当点B在第一象限时，过A作AC⊥x轴于C，过B作BD⊥AC于D，则AC=1，OC=3，
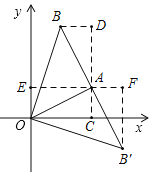
易得△ABD≌△OAC（AAS），
∴AC=BD=1，AD=OC=3，
∴B（2，4）；
当点B'在第四象限时，过A作AE⊥y轴于E，过B'作B'F⊥AE于F，则OE=1，AE=3，
易得△AOE≌△B'AF（AAS），
∴AF=OE=1，B'F=AE=3，
∴B'（4，-2），
故答案为：（2，4）或（4，-2）．
练习册系列答案
相关题目
【题目】小亮与小明做投骰子（质地均匀的正方体）的实验与游戏．
（1）在实验中他们共做了50次试验，试验结果如下：
朝上的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现的次数 | 10 | 9 | 6 | 9 | 8 | 8 |
①填空：此次实验中，“1点朝上”的频率是 ；
（2）在游戏时两人约定：每次同时掷两枚骰子，如果两枚骰子的点数之和超过6，则小亮获胜，否则小明获胜．则小亮与小明谁获胜的可能性大？试说明理由．
