Question

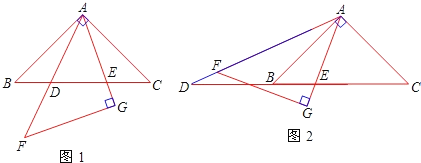
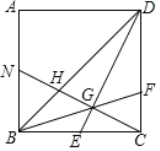
【题目】如图，正方形ABCD中，E为BC的中点，CG⊥DE于G，BG延长交CD于点F，CG延长交BD于点H，交AB于N.下列结论：①DE=CN；②；③S△DEC=3S△BNH；④∠BGN=45°；⑤.其中正确结论的个数有( )

A.2个B.3个C.4个D.5个

Answer 1

【答案】D

【解析】

根据题目已知证明可判断①正确；证明可判断②正确；过H点作，利用，求解即可判断③正确；添加辅助线过B作BP⊥CN于P，BQ⊥DG，交DE的延长线于E，利用△BNC≌△CED，证得△BPN≌△BQE，即可判断④正确；连接N，E，设,则,,利用勾股定理求出CN，CE的长，然后根据的面积求出GE，GN，再证，利用相似三角形对应边成比例，求出BG，BF的长，即可得⑤正确．

解：①∵在正方形ABCD中，，,

∴

即：

∴（ASA）

∴CN= DE，故①正确；

②∴在正方形ABCD中， ，

∴，

∴，

∵，E为BC的中点， 四边形ABCD是正方形

∴，

∴，故②正确；

③如下图示，过H点作，

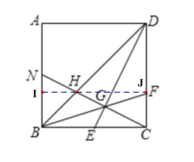
∴根据，有，

则：

∴，

即是：，故③正确 ；

④过B作BP⊥CN于P，BQ⊥DG，交DE的延长线于E，

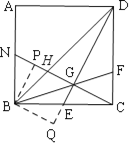
∴∠BPC=∠BQD=∠PGQ=90°，
∴四边形PBQG是矩形，
∴∠PBQ=90°，
∵∠ABC=90°，
∴∠NBP=∠QBE，
由①得：△BNC≌△CED，
∴EC=BN，
∵E是BC的中点，
∴BE=EC，
∴BE=BN，
∵∠BPN=∠BQE=90°，
∴△BPN≌△BQE，
∴BP=BQ，
∴四边形PBQG是正方形，
∴∠BGE=45°，故④正确；

⑤如图示，连接N，E

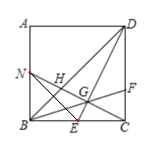
设,则,,

∵CG⊥DE，

∴，

，

由的面积可得：

化简得：，

∴，

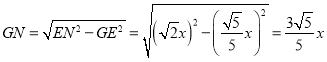则有：

∴ ，

∵，

∴，

∴，

∴，

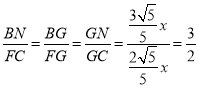则，

，

并∵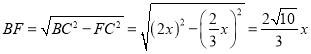

∴

∴，故⑤正确．

综上所述，故选：D．