Question

【题目】先化简分式： ，再从不等式组 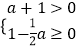的解集中选出合适的整数作为a的值，代入求值.

Answer 1

【答案】解：原式= ÷
=
= .
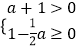∵ 的解集是-1<a≤2，
其整数解为0,1,2；由于a≠0,±2，
∴a只能取1，故当a=1时，原式= .
【解析】分式运算里有括号的先算括号，分子和分母中能因式分解的要因式分解再作加减法或乘除法．对分式求值时，取的未知数的值，一定要使分式有意义.
【考点精析】本题主要考查了分式方程的解和分式方程的应用的相关知识点，需要掌握分式方程无解（转化成整式方程来解,产生了增根;转化的整式方程无解）；解的正负情况:先化为整式方程,求整式方程的解；列分式方程解应用题的步骤：审题、设未知数、找相等关系列方程、解方程并验根、写出答案（要有单位）才能正确解答此题．