题目内容
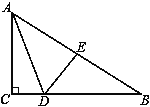
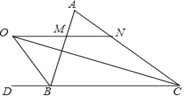
【题目】如图,已知在△ABC中,△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.
求证:(1)MO=MB;(2)MN=CN﹣BM.
【答案】见解析
【解析】
【试题分析】(1)因为OB是∠ABD的平分线,根据角平分线的定义,得∠0BD=∠OBM,因为MN∥BC,根据两直线平行,内错角相等,得∠0BD=∠BOM,等量代换得:∠OBM=∠BOM,
根据等角对等边,得:MO=MB
(2)因为OC是∠ACB的平分线,根据角平分线的定义,得∠BCO=∠ACO
因为MN∥BC,根据两直线平行,内错角相等,得∠BCO=∠NOC,等量代换得:∠NOC=∠NCO
根据等角对等边,得:NO=NC,由图可知,MN=NO-MO,等量代换得,MN=CN-BM.
【试题解析】
(1)∵OB是∠ABD的平分线.
∴∠0BD=∠OBM.
∵MN∥BC.
∴∠0BD=∠BOM.
∴∠OBM=∠BOM.
∴MO=MB.
(2)∵OC是∠ACB的平分线.
∴∠BCO=∠ACO.
∵MN∥BC.
∴∠BCO=∠NOC.
∴∠NOC=∠NCO.
∴NO=NC.
∵MN=NO-MO.
∴MN=CN-BM.

练习册系列答案
相关题目