题目内容
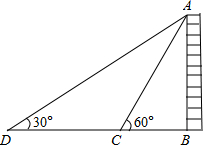
如图，一条河有一段笔直的河岸，从南岸可以望到北岸的电视塔CD，并且在南岸某点处测得点C的仰角为31°，测量者在南岸，工具有皮尺和测角仪（可测水平角和仰、俯角），不过河怎样测出电视塔的高度？
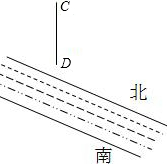
因为在南岸有点测得点C的仰角为31°，所以在南岸上可取
点A和点B，使得仰角∠CAD=30°，水平角∠DAB=90°；
在射线AB上找一点E，使得水平角∠AED=45°，
用皮尺量出AE的长度为a米．
由两个Rt△ADC，Rt△EAD得：CD=
DA=
AE=
a（米）．
所以电视塔的高度为
a（米）．
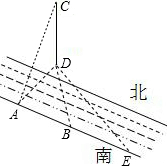
点A和点B，使得仰角∠CAD=30°，水平角∠DAB=90°；
在射线AB上找一点E，使得水平角∠AED=45°，
用皮尺量出AE的长度为a米．
由两个Rt△ADC，Rt△EAD得：CD=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
所以电视塔的高度为
| ||
| 3 |
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
是43度．1s后，火箭到达B点，此时测得BC的距离是6.13km，仰角为45.54°，解答下列问题：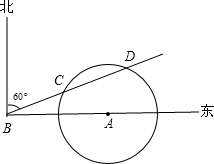
北偏东60°的BD方向移动，在距离台风中心130km内的地方都要受到其影响．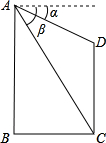
______m2（结果保留根号）．