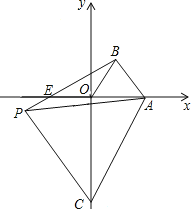
ЬтФПФкШн
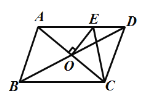
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAЕФзјБъЪЧЃЈaЃЌ0ЃЉЃЈaЃО0ЃЉЃЌЕуCЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌЕуCдкyжсЩЯвЦЖЏЪБЃЌЪМжеБЃГжЁїACPЪЧЕШБпШ§НЧаЮЃЌЕБЕуCвЦЖЏЕНЕуOЪБЃЌЕУЕНЕШБпЁїAOBЃЈДЫЪБЕуPгыЕуBжиКЯЃЉЃЎ
ЃЈ1ЃЉЕуCдквЦЖЏЕФЙ§ГЬжаЃЌЕБЕШБпШ§НЧаЮACPЕФЖЅЕуPдкЕкШ§ЯѓЯоЪБЃЈШчЭМЫљЪОЃЉЃЌЧѓжЄЃКЁїAOCЁеЁїABPЃЛ
ЃЈ2ЃЉШєЕуPдкЕкШ§ЯѓЯоЃЌBPНЛxжсгкЕуEЃЌЧвЁЯACOЃН20ЁуЃЌЧѓЁЯPAEЕФЖШЪ§КЭEЕуЕФзјБъЃЛ
ЃЈ3ЃЉШєЁЯAPBЃН30ЁуЃЌдђЕуPЕФКсзјБъЮЊЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћНтЮіЃЛЃЈ2ЃЉЁЯPAEЃНЁЯOACЉЁЯCAPЃН10ЁуЃЌEЃЈЉaЃЌ0ЃЉЃЛЃЈ3ЃЉЉaЛђ2aЃЎ
ЁОНтЮіЁП
(1) ЯШХаЖЯГіЁЯOAC=ЁЯBAP, НјЖјЕУГіНсТл;
(2) РћгУжБНЧШ§НЧаЮЕФаджЪЕУГіЁЯOAC, НјЖјЕУГіЁЯPAE, дйРћгУШЋЕШШ§НЧаЮЕФаджЪЕУГіЁЯAPB,РћгУШ§НЧаЮЕФЭтНЧЕУГіЁЯAEB=30![]() , МДПЩЕУГіНсТл;
, МДПЩЕУГіНсТл;
(3) ЗжЕуCдкyжсИКАыжсКЭе§АыжсЩЯ,ХаЖЯГіЕуPдкxжсЩЯ, МДПЩЕУГіНсТл.
ЃЈ1ЃЉжЄУїЃКЁпЁїAOBКЭЁїACPЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрOAЃНABЃЌAPЃНACЃЌЁЯOABЃНЁЯCAPЃН60Ёу
ЁрЁЯOACЃНЁЯBAPЃЌ
дкЁїAOCКЭЁїABPжаЃЌ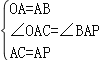 ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїABPЃЈSASЃЉЃЌ
ЃЈ2ЃЉНтЃКЁпЁЯACOЃН20ЁуЃЌ
ЁрЁЯOACЃН90ЁуЉ20ЁуЃН70ЁуЃЌ
ЁпЁЯCAPЃН60ЁуЃЌ
ЁрЁЯPAEЃНЁЯOACЉЁЯCAPЃН10ЁуЃЛ
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЌ
ЁрЁЯABPЃНЁЯAOCЃН90ЁуЃЌЁЯACOЃНЁЯAPBЃН20ЁуЃЌ
ЁрЁЯAEBЃНЁЯAPB+ЁЯPAEЃН20Ёу+10ЁуЃН30ЁуЃЌ
ЁпAЃЈaЃЌ0ЃЉЃЌ
ЁрOAЃНaЃЌ
ЁрABЃНOAЃНaЃЌ
дкRtЁїABEжаЃЌAEЃН2ABЃН2aЃЌ
ЁрOEЃНAEЉOAЃНaЃЌ
ЁрEЃЈЉaЃЌ0ЃЉЃЛ
ЃЈ3ЃЉ
ЕБЕуCдкyжсИКАыжсЩЯЪБЃЌЕБЁЯAPBЃН30ЁуЪБЃЌ
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЌ
ЁрЁЯABPЃНЁЯAOCЃН90ЁуЃЌ
ЁпЁЯOABЃН60ЁуЃЌ
ЁрЁЯAEBЃН30ЁуЃНЁЯAPBЃЌ
ЁрЕуPКЭЕуEжиКЯЃЌ
МДЃКЕуPдкxжсЩЯЃЌ
дкRtЁїABEжаЃЌABЃНaЃЌ
ЁрAPЃН2ABЃН2aЃЌ
ЁрOPЃНAPЉOAЃНaЃЌ
ЁрPЃЈЉaЃЌ0ЃЉЃЛ
ЕБЕуCдкyжсе§АыжсЪБЃЌ
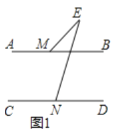
ШчЭМЃЈзЂЃКЮЊСЫЫЕУїЕуPвВдкxжсЩЯЃЌзїЕФЭМаЮЃЌВЛБъзМЃЉ
ЁпЁЯAOBЃН60ЁуЃЌ
ЁрЁЯAPBЃН![]() ЁЯAOBЃЌ
ЁЯAOBЃЌ
ЁрЕуPдквдЕуOЮЊдВаФЃЌOAЮЊАыОЖЕФдВЩЯЃЌ
ЁрOPЃНOAЃЌ
дкЁїAOCКЭЁїPOCжаЃЌ ЃЌ
ЃЌ
ЁрЁїAOCЁеЁїPOCЃЌ
ЁрЁЯACOЃНЁЯPCOЃЌ
ЁпЁЯACPЃН60ЁуЃЌ
ЁрЁЯACOЃНЁЯPCOЃЌ
ЁрOCЁЭAPЃЌ
ЁпOCЁЭOAЃЌЁрЕуPдкxжсЩЯЃЌ
ЁрЕуPЕФКсзјБъЮЊЉaЃЌ
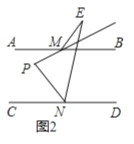
ЕБЕуCдкyжсАыжсЩЯЪБЃЌЁЯAPBЃН30ЁуЃЌШчЭМ1ЃЌЃЈзЂЃКЮЊСЫЫЕУїЕуBКЭFжиКЯЃЌзїЕФЭМаЮЃЌВЛБъзМЃЉ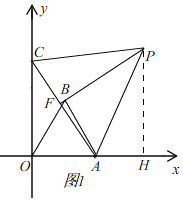
гЩЃЈ1ЃЉжЊЃЌЁїAOCЁеЁїABPЃЈSASЃЉЃЌ
ЁрЁЯABPЃНЁЯOACЃН90ЁуЃЌ
ЁпдкЕШБпШ§НЧаЮACPжаЃЌЁЯCAPЃН60ЁуЃЌ
ЁпЁЯAPBЃН30ЁуЃЌ
ЁрЁЯAFPЃН90ЁуЃЌ
ЁрЕуBКЭFжиКЯЃЌ
ЁрABЃН![]() ACЃН
ACЃН![]() APЃЌ
APЃЌ
ЁпOAЃНABЃЌ
ЁрOAЃН![]() APЃЌ
APЃЌ
Й§ЕуPзїPHЁЭOAгкHЃЌ
ЁрЁЯPAHЃН60ЁуЃЌ
ЁрAHЃН![]() APЃЌ
APЃЌ
ЁрAHЃНOAЃЌ
ЁрAHЃН2OAЃЌ
ЁпAЃЈaЃЌ0ЃЉЃЌ
ЁрOAЃНaЃЌ
ЁрAHЃН2aЃЌ
ЁрЕуPЕФКсзјБъЮЊ2aЃЌ
ЙЪД№АИЮЊЃКЉaЛђ2aЃЎ