��Ŀ����
����Ŀ����֪����MON=80�㣬OEƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ��㣨A��B��C�����O �غϣ�������AC������OE�ڵ�D�����OAC=x�㣮
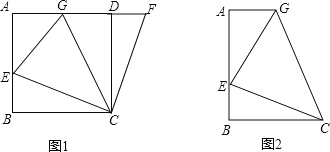
��1����ͼ1����AB��ON���١�ABO�Ķ�������������������
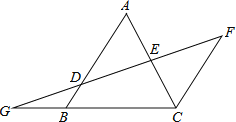
����ͼ2������BAD=��ABDʱ������x��ֵ��Ҫ˵�����ɣ���
��2����ͼ3����AB��OM�����Ƿ����������X��ֵ��ʹ�á�ADB����������ȵĽǣ������ڣ�ֱ��д��x��ֵ���������ڣ�˵�����ɣ����Լ���ͼ��

���𰸡���1���١�ABO�Ķ���400��x=600��2������������x��x=100��x=250��x=400
�������������������1��������������MON=80����OEƽ����MON���ɵ���AOB=��NOB =40�����ٸ���AB��ON������ABO=��NOB =40��;���������Ľ��۽��������BAD=��ABD �������2=400����4=800���ٸ��������ε��ڽǺͿ����x=600��2���ֵ���D���߶�OB��ʱ�� ����D������BE��ʱ,����������ۣ�����������x��x=10����x=25����x=40��
�����������1��
�١�ABO�Ķ�����40��
�ڡߡ�MON=80������OEƽ����MON�����1=��2=40����
����AB//ON�����3=��1=40��
�ߡ�BAD=��ABD�����BAD=40����
���4=80����
���OAC=600����x=60��
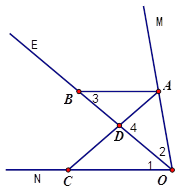
��2������С��4�֣�ÿ��1�֣�ȫ��4�֣�
����������x��
x=10��
x=25��
x=40��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�