题目内容
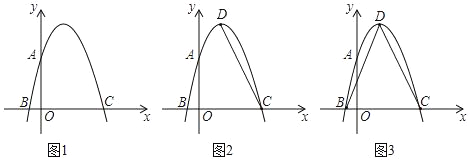
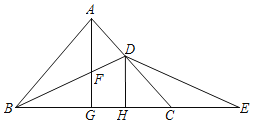
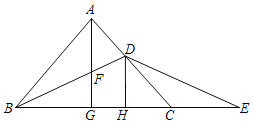
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,点E是BC延长线上的一点,且BD=DE.点G是线段BC的中点,连结AG,交BD于点F,过点D作DH⊥BC,垂足为H.
(1)求证:△DCE为等腰三角形;
(2)若∠CDE=22.5°,DC=![]() ,求GH的长;
,求GH的长;
(3)探究线段CE,GH的数量关系并用等式表示,并说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)CE=2GH,理由见解析.
;(3)CE=2GH,理由见解析.
【解析】
(1)根据题意可得∠CBD=![]() ∠ABC=
∠ABC=![]() ∠ACB,,由BD=DE,可得∠DBC=∠E=
∠ACB,,由BD=DE,可得∠DBC=∠E=![]() ∠ACB,根据三角形的外角性质可得∠CDE=
∠ACB,根据三角形的外角性质可得∠CDE=![]() ∠ACB=∠E,可证△DCE为等腰三角形;
∠ACB=∠E,可证△DCE为等腰三角形;
(2)根据题意可得CH=DH=1,△ABC是等腰直角三角形,由等腰三角形的性质可得BG=GC,BH=HE=![]() +1,即可求GH的值;
+1,即可求GH的值;
(3)CE=2GH,根据等腰三角形的性可得BG=GC,BH=HE,可得GH=GC﹣HC=GC﹣(HE﹣CE)=![]() BC﹣
BC﹣![]() BE+CE=
BE+CE=![]() CE,即CE=2GH
CE,即CE=2GH
证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
∵BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]() ∠ACB,
∠ACB,
∵BD=DE,
∴∠DBC=∠E=![]() ∠ACB,
∠ACB,
∵∠ACB=∠E+∠CDE,
∴∠CDE=![]() ∠ACB=∠E,
∠ACB=∠E,
∴CD=CE,
∴△DCE是等腰三角形
(2)
∵∠CDE=22.5°,CD=CE=![]() ,
,
∴∠DCH=45°,且DH⊥BC,
∴∠HDC=∠DCH=45°
∴DH=CH,
∵DH2+CH2=DC2=2,
∴DH=CH=1,
∵∠ABC=∠DCH=45°
∴△ABC是等腰直角三角形,
又∵点G是BC 中点
∴AG⊥BC,AG=GC=BG,
∵BD=DE,DH⊥BC
∴BH=HE=![]() +1
+1
∵BH=BG+GH=CG+GH=CH+GH+GH=![]() +1
+1
∴1+2GH=![]() +1
+1
∴GH=![]()
(3)CE=2GH
理由如下:∵AB=CA,点G 是BC的中点,
∴BG=GC,
∵BD=DE,DH⊥BC,
∴BH=HE,
∵GH=GC﹣HC=GC﹣(HE﹣CE)=![]() BC﹣
BC﹣![]() BE+CE=
BE+CE=![]() CE,
CE,
∴CE=2GH