题目内容
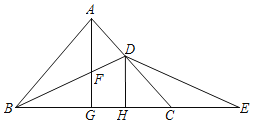
【题目】已知△ABC的三个角是∠A，∠B，∠C ，它们所对的边分别是a，b，c.①c2－a2＝b2；②∠A＝
∠B＝
∠C；③c＝
a＝b；④a＝2，b＝2 ，c＝
.上述四个条件中，能判定△ABC 为直角三角形的有( )
A. 1个 B. 2个
C. 3个 D. 4个
【答案】C
【解析】
根据勾股定理逆定理、三角形的内角和逐一进行判断即可得.
①由c2－a2＝b2，可得c2=a2+b2，故可判断三角形ABC是直角三角形；
②∵∠A＝
∠B＝
∠C，∴∠B=2∠A，∠C=3∠A，
∵∠A+∠B+∠C=180°，∴∠A=30°，∠B=60°，∠C=90°，
∴△ABC是直角三角形；
③∵c＝
a＝b，∴a=b，
∴a2+b2=2a2=c2，∴△ABC是直角三角形；
④∵a＝2，b＝2 ，c＝
，
∴a2+b2=12≠c2，
∴△ABC不是直角三角形，
故选C.
阅读快车系列答案【题目】近年来，共享单车逐渐成为高校学生喜爱的“绿色出行”方式之一，自2016年国庆后，许多高校均投放了使用手机支付就可随取随用的共享单车．某高校为了解本校学生出行使用共享单车的情况，随机调查了某天部分出行学生使用共享单车的情况，并整理成如下统计表．
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
（1）这天部分出行学生使用共享单车次数的中位数是 ，众数是 ，该中位数的意义是 ；
（2）这天部分出行学生平均每人使用共享单车约多少次？（结果保留整数）
（3）若该校某天有1500名学生出行，请你估计这天使用共享单车次数在3次以上（含3次）的学生有多少人？
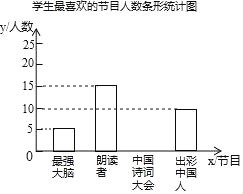
【题目】为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：根据以上提供的信息，解答下列问题：
节目 | 人数（名） | 百分比 |
最强大脑 | 5 | 10% |
朗读者 | 15 | b% |
中国诗词大会 | a | 40% |
出彩中国人 | 10 | 20% |
（1）x= ，a= ，b= ；
（2）补全上面的条形统计图；
（3）在喜爱《最强大脑》的学生中，有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动，请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率．
