题目内容
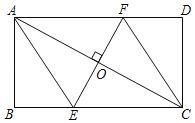
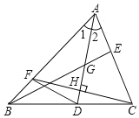
【题目】如图所示,在△ABC中,AD是∠BAC的平分线,G是AD上一点,且AG=DG,连接BG并延长BG交AC于E,又过C作AD的垂线交AD于H,交AB为F,则下列说法:
①D是BC的中点;
②BE⊥AC;
③∠CDA>∠2;
④△AFC为等腰三角形;
⑤连接DF,若CF=6,AD=8,则四边形ACDF的面积为24.
其中正确的是________(填序号).
【答案】③④⑤
【解析】
①中依据已知条件无法判断BD=DC,可判断结论错误;
②若BE⊥AC,则∠BAE+∠ABE=90°,结合已知条件可判断;
③根据三角形外角的性质可判断;
④证明△AHF≌△AHC,即可判断;
⑤四边形ACDF的面积等于△AFC的面积与△DFC的面积之和,据此可判断.
解:①根据已知条件无法判断BD=DC,所以无法判断D是BC的中点,故错误;
②只有∠BAE和∠BAC互余时才成立,故错误;
③正确.∵∠ADC=∠1+∠ABD,∠1=∠2,
∴∠ADC>∠2,故②正确;
④正确.∵∠1=∠2,AH=AH,∠AHF=∠AHC=90°,
∴△AHF≌△AHC(ASA),
∴AF=AC,△AFC为等腰三角形,故④正确;
⑤正确.∵AD⊥CF,
![]() .
.
故答案为:③④⑤.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目