题目内容
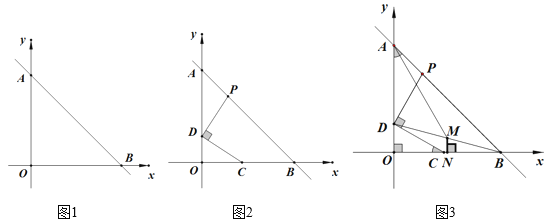
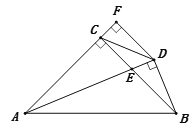
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE交AE延长线于D,DF⊥AC交AC的延长线于F,连接CD,给出四个结论:① ∠FDC=22.5°; ② 2BD=AE;③ AC+CE=AB; ④ AB-BC=2FC.其中正确的结论有( ) 个
A.1B.2C.3D.4
【答案】D
【解析】
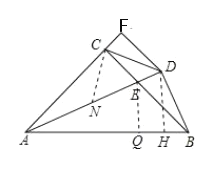
过E作EQ⊥AB于Q,作∠ACN=∠BCD,交AD于N,过D作DH⊥AB于H,根据角平分线性质求出CE=EQ,DM=DH,根据勾股定理求出AC=AQ,AM=AH,根据等腰三角形的性质和判定求出BQ=QE,即可求出③;根据三角形外角性质求出∠CND=45°,证△ACN≌△BCD,推出CD=CN,即可求出①②;证△DCM≌△DBH,得到CM=BH,AM=AH,即可求出④.
解:如图,
∵∠ACB=90°,AE平分∠CAB,
∴CE=EQ,
∵∠ACB=90°,AC=BC,
∴∠CBA=∠CAB=45°,
∵EQ⊥AB,
∴∠EQA=∠EQB=90°,
由勾股定理得:AC=AQ,
∴∠QEB=45°=∠CBA,
∴EQ=BQ,
∴AB=AQ+BQ=AC+CE,
∴③正确;
作∠ACN=∠BCD,交AD于N,
∵∠CAD=![]() ∠CAB=22.5°=∠BAD,
∠CAB=22.5°=∠BAD,
∴∠ABD=90°22.5°=67.5°,
∴∠DBC=67.5°45°=22.5°=∠CAD,
∴∠DBC=∠CAD,
∵AC=BC,∠ACN=∠DCB,
∴△ACN≌△BCD,
∴CN=CD,AN=BD,
∵∠ACN+∠NCE=90°,
∴∠NCB+∠BCD=90°,
∴∠CND=∠CDA=45°,
在![]() 中,∠AFD=90°,∠FCD=22.5°,
中,∠AFD=90°,∠FCD=22.5°,
∴∠FDA=67.5°,
∵∠FDC=∠FDA-∠CDA=22.5°,故①正确;
∴∠ACN=45°22.5°=22.5°=∠CAN,
∴AN=CN,
∴∠NCE=∠AEC=67.5°,
∴CN=NE,
∴CD=AN=EN=![]() AE,
AE,
∵AN=BD,
∴BD=![]() AE,
AE,
故②正确;
过D作DH⊥AB于H,
∵∠MCD=∠CAD+∠CDA=67.5°,
∠DBA=90°∠DAB=67.5°,
∴∠MCD=∠DBA,
∵AE平分∠CAB,DM⊥AC,DH⊥AB,
∴DM=DH,在△DCM和△DBH中∠M=∠DHB=90°,∠FCD=∠DBA,DF=DH,
∴△DCF≌△DBH,
∴BH=CF,由勾股定理得:AF=AH,
∴![]() ,
,
∴AC+AB=2AF,AC+AB=2AC+2CF,ABAC=2CF,
∵AC=CB,
∴ABCB=2CF,
∴④正确;
故答案选:D.