题目内容
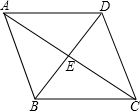 如图所示,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求:
如图所示,四边形ABCD是边长为13cm的菱形,其中对角线BD长10cm,求:(1)对角线AC的长度为
(2)菱形ABCD的面积为
分析:(1)因为菱形的对角线互相垂直平分,可利用勾股定理求得AE或CE的长,从而求得AC的长;
(2)利用菱形的面积公式:两条对角线的积的一半求得面积.
(2)利用菱形的面积公式:两条对角线的积的一半求得面积.
解答:解:(1)∵四边形ABCD为菱形
∴∠AED=90°
∵DE=
BD=
×10=5(cm)
∴AE=
=
=12(cm)
∴AC=2AE=2×12=24(cm)
(2)S菱形ABCD=S△ABD+S△BDC=
BD•AE+
BD•CE
=
BD(AE+CE)
=
BD•AC=
×10×24
=120(cm2)
∴∠AED=90°
∵DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AE=
| AD2-DE2 |
| 132-52 |
∴AC=2AE=2×12=24(cm)
(2)S菱形ABCD=S△ABD+S△BDC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=120(cm2)
点评:主要考查菱形的面积公式:两条对角线的积的一半和菱形的对角线性质,综合利用了勾股定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
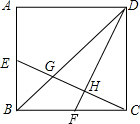
 21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G.
21、如图所示,四边形ABCD是平行四边形,E,F分别在AD,CB的延长线上,且DE=BF,连接FE分别交AB,CD于点H,G. 12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )
12、如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )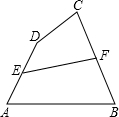 如图所示,四边形ABCD中,E、F分别为AD、BC的中点.
如图所示,四边形ABCD中,E、F分别为AD、BC的中点.