ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉ![]() x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌгыжБЯпyЃНxНЛгкЕуCЃЎдкЯпЖЮOAЩЯЃЌЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуAГіЗЂЯђЕуOзідШЫйдЫЖЏЃЌЕБЕуPЁЂQЦфжавЛЕуЭЃжЙдЫЖЏЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЗжБ№Й§ЕуPЁЂQзїxжсЕФДЙЯпЃЌНЛжБЯпABЁЂOCгкЕуEЁЂFЃЌСЌНгEFЃЎШєдЫЖЏЪБМфЮЊtУыЃЌдкдЫЖЏЙ§ГЬжаЫФБпаЮPEFQзмЮЊОиаЮЃЈЕуPЁЂQжиКЯГ§ЭтЃЉЃЎ
x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌгыжБЯпyЃНxНЛгкЕуCЃЎдкЯпЖЮOAЩЯЃЌЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуAГіЗЂЯђЕуOзідШЫйдЫЖЏЃЌЕБЕуPЁЂQЦфжавЛЕуЭЃжЙдЫЖЏЪБЃЌСэвЛЕувВЭЃжЙдЫЖЏЃЎЗжБ№Й§ЕуPЁЂQзїxжсЕФДЙЯпЃЌНЛжБЯпABЁЂOCгкЕуEЁЂFЃЌСЌНгEFЃЎШєдЫЖЏЪБМфЮЊtУыЃЌдкдЫЖЏЙ§ГЬжаЫФБпаЮPEFQзмЮЊОиаЮЃЈЕуPЁЂQжиКЯГ§ЭтЃЉЃЎ
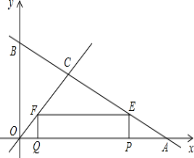
ЃЈ1ЃЉЧѓЕуPдЫЖЏЕФЫйЖШЪЧЖрЩйЃП
ЃЈ2ЃЉЕБtЮЊЖрЩйУыЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃП
ЁОД№АИЁПЃЈ1ЃЉЕуPдЫЖЏЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЛЃЈ2ЃЉtЃН2Лђ4ЃЛ
ЁОНтЮіЁП
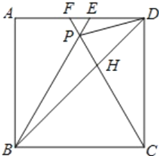
ЃЈ1ЃЉЯШЧѓЕУAЃЌBСНЕузјБъЃЌЕУЕН![]() ЕФжЕЃЌдйИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЕУЕНAPгыEPЕФБШжЕЃЌНјЖјЕУЕНЕуPЕФЫйЖШЃЛ
ЕФжЕЃЌдйИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЕУЕНAPгыEPЕФБШжЕЃЌНјЖјЕУЕНЕуPЕФЫйЖШЃЛ
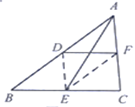
ЃЈ2ЃЉЗжQЃЌPСНЕуЯргіЧАКѓСНжжЧщПіНјааЬжТлЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌгЩгУЙигкtЕФЪНзгБэЪОИїЯпЖЮЕФГЄЃЌШЛКѓЧѓГіtЕФжЕМДПЩ.
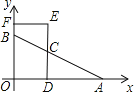
НтЃКЃЈ1ЃЉЁпжБЯпyЃНЉ![]() x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌ
x+4гызјБъжсЗжБ№НЛгкЕуAЁЂBЃЌ
ЁрxЃН0ЪБЃЌyЃН4ЃЌyЃН0ЪБЃЌxЃН8ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБtУыЪБЃЌQOЃНFQЃНtЃЌдђEPЃНtЃЌ
ЁпEPЁЮBOЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрAPЃН2tЃЌ
ЁпЖЏЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуOГіЗЂЯђЕуAзідШЫйдЫЖЏЃЌ
ЁрЕуPдЫЖЏЕФЫйЖШЪЧУПУы2ИіЕЅЮЛГЄЖШЃЛ
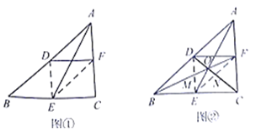
ЃЈ2ЃЉШчЭМЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌ
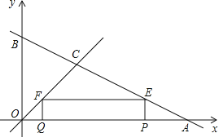
дђЁпOQЃНFQЃНtЃЌPAЃН2tЃЌ
ЁрQPЃН8ЉtЉ2tЃН8Љ3tЃЌ
Ёр8Љ3tЃНtЃЌ
НтЕУЃКtЃН2ЃЛ
ШчЭМ2ЃЌЕБPQЃНPEЪБЃЌОиаЮPEFQЮЊе§ЗНаЮЃЌ
ЁпOQЃНtЃЌPAЃН2tЃЌ
ЁрOPЃН8Љ2tЃЌ
ЁрQPЃНtЉЃЈ8Љ2tЃЉЃН3tЉ8ЃЌ
ЁрtЃН3tЉ8ЃЌ
НтЕУЃКtЃН4ЃЛ

ЁОЬтФПЁПжаЛЊЮФУїЃЌдДдЖСїГЄЃЌжаЛЊККзжЃЌдЂвтЩюЙу.ЮЊДЋГажаЛЊгХауДЋЭГЮФЛЏЃЌФГжабЇЕТг§ДІзщжЏСЫвЛДЮШЋаЃ2000УћбЇЩњВЮМгЕФЁАККзжЬ§аДЁБДѓШќ.ЮЊСЫНтБОДЮДѓШќЕФГЩМЈЃЌбЇаЃЕТг§ДІЫцЛњГщШЁСЫЦфжа200УћбЇЩњЕФГЩМЈзїЮЊбљБОНјааЭГМЦЃЌжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэЃК
ГЩМЈxЃЈЗжЃЉЗжЪ§ЖЮ | ЦЕЪ§ЃЈШЫЃЉ | ЦЕТЪ |
50Ёмx<60 | 10 | 0.05 |
60Ёмx<70 | 30 | 0.15 |
70Ёмx<80 | 40 | 0.2 |
80Ёмx<90 | m | 0.35 |
90Ёмx<100 | 50 | n |
ЦЕЪ§ЗжВМжБЗНЭМ

ИљОнЫљИјЕФаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉm=________ЃЛn=________ЃЛ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉет200УћбЇЩњГЩМЈЕФжаЮЛЪ§ЛсТфдк________ЗжЪ§ЖЮЃЛ
ЃЈ4ЃЉШєГЩМЈдк90ЗжвдЩЯЃЈАќРЈ90ЗжЃЉЮЊЁАгХЁБЕШЃЌЧыФуЙРМЦИУаЃВЮМгБОДЮБШШќЕФ2000УћбЇЩњжаГЩМЈЪЧЁАгХЁБЕШЕФдМгаЖрЩйШЫЃП